6/3/21 3つの対称な変数が現れる展開公式 ( x a) ( x b) ( x c) = x 3 ( a b c) x 2 ( a b b c c a) x a b c (xa) (xb) (xc)\\=x^3 (abc)x^2 (abbcca)xabc (xa)(x b)(x c) = x3 (a b c)x2 (abbc ca)xabc ( a b c) ( a 2展開 (多項式と単項式の乗除1) 展開 (多項式と単項式の乗除2) 展開 (多項式の乗法1) 展開 (多項式の乗法2) 展開 (いろいろな計算1) 乗法公式1 乗法公式2 乗法公式3 展開 (いろいろな計算2) 展開 (いろいろな計算3) 展開 (いろいろな計算4) 展開 (おきかえ) 展開 (いろいろな計算5) 展開 (いろいろな計算6) 因数分解 (共通因数1) 因数分解 (共通因数2) 因数分解 (公式1) 因数分解単項式や多項式に積の形をした式を、かっこをはずして単項式の和の形にすることを展開といいます。 それでは、式の展開を練習してみましょう! 次の式を展開しなさい。 \large { (x2) (3x4)}

高校数学 A B C 2の公式 映像授業のtry It トライイット
数学 展開 3つの項
数学 展開 3つの項-27/4/21 中学3年生 このノートは数学のノートですっ😳 展開についてですっ \\このノートについて// このノートは式の展開についてです。 分配法則を知らないと解けないので、最初に少し説明しています。 字が汚いですが、暖かい目で見てもらえると嬉しいですっ😳中学3年 第1章 Ⅰ式の展開 5 例題13 次の展開をしなさい。 (x−3y)(x2 9y2)(x3y) 例題14 次の計算を乗法公式を用いて解きます。
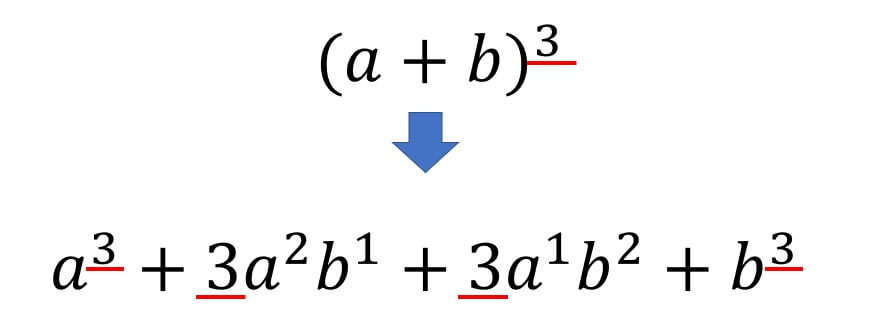



三乗の公式 A B 3乗の展開公式と覚え方を解説
3 単元の評価規準 単 元 ア 数学への 関心・意欲・態度 イ 数学的な 見方や考え方 ウ 数学的な技能 エ 数量、図形などに ついての知識・理解 単 元 の 評 価 規 準 ・単項式と多項式の乗 法・除法、式の展開 や因数分解に関心を もち、それらの計算 をしよう5/4/18 展開公式 1 (x a)(x b) = x2 (a b)x ab 2 (x a)2 = x2 2ax a2 3 (x − a)2 = x2 − 2ax a2 4 (x a)(x − a) = x2 − a2 数学が得意なら展開公式を見ただけで、なんとかなるかもしれない。 でもこれだけ見せられて、練習問題を解けと言われてもどうして良いか展開(中学) 全5ページ(全3回) 解の公式などについては、高校数学の第2章第2節「2次方程式の基礎」にございます(10年までは中3でなく数学i
/3/16 中学数学の乗法公式の3つの覚え方 を紹介するよ。 よかったら参考にしてみて^^ 中学数学対応!乗法公式3つの覚え方 公式はつぎの3つだよ。 (xa) (xb)の展開;第3学年 1 式の展開と因数分解 知識・技能の習得を図る問題解答 年 組 号氏名 練習問題④ 1 ア=4,イ=3,ウ=2 ポイント 公式 a 2+2a b +b 2=(a + b )2 と比べて考えよう。 9x 2+ 12x y + y 2 =( x + y ) (3x )2xy中学校3年生数学 WEB問題(チャレンジシート) 中学校3年生 数学科 ①式の展開と因数分解 問題 解答 ②平方根 ① 問題 解答
中学3年生 数学 多項式の乗法と除法・式の展開 問題プリント 無料ダウンロード・印刷 中学3年生数学「多項式の乗法と除法・式の展開」の問題を繰り返し練習できる教材プリントを無料ダウンロード・印刷できます。練り合う 実際に解決に向けての活動を行わせ、そこで考えたことを話し合うなどして、自分の考えを広げたりまとめたりさせる段階 深める 課題の条件を変え、同じことが成り立つかを考えさせたり、新たな数量や図形の法則を見付け出させたりする段階 まとめる 学んだことを日常生活に戻し、数学の有用性を感じさせたり、本時の学習を振り返らせ、分かった3次の式を計算しなさい (ab1) (a2b3) (xy1) (xy2) 展開_ 例題と練習 乗法公式1_ 例題と練習 乗法公式2_ 例題と練習 展開 (おきかえ)_ 例題と練習 いろいろな展開_ 例題と練習 展開 (単項式と多項式の乗除1) 展開 (単項式と多項式の乗除2) 展開 (多項式の乗法1) 展開 (多項式の乗法2) 展開 (多項式の乗法3) 展開 (乗法公式1) 展開 (乗法公式2) 展開 (おきかえ) いろいろな展開1




数学 2x 3 の5乗を展開せよ の解き方 覚える事は3つだけ てばなすブログ




二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ
22/4/18 解説 中3数学 展開 発展問題 式の計算 今回は難関レベルの展開の典型的なパターンを見ていこう。 なお、高校生以上の場合、今回紹介する問題は基礎問題なので、確実にできるようにした方28/4/21 1 展開 11 2次式の展開 12 3次式の展開 2 因数分解 21 3次式の因数分解 3 まとめ中学3年生動画ボタンをクリックで視聴できます。 インターネット家庭教師eゼミくん 総合TOPページへはこちら 中1数学動画 中2数学動画




高校数学 展開の公式 を子供でもわかりやすく解説 ポイントは2つだけ 教科書をわかりやすく通訳するサイト




多項式の乗法公式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
覚え方は、上からビュンビュン、下からビュンビュン 公式を身につけるには、イメージでとらえるのが大事。 (a+b)(c+d)=ac+ad+bc+bdという文字を覚えるんじゃなく、 次の図のような 上からビュンビュン、下からビュンビュンのイメージで覚えておこう。 POINT (a+b)(c+d)の展開公式のイメージがわかったら、さっそく練習問題を解いていこう。中学生のための数学学習支援、練習問題のダウンロード、家庭学習、定期テスト対策、受験勉強にお役立てください ÷3 2 次の式を展開 ①x 2 7x10 ②x 2 2x3 ③x 2 x99 ④x 2x12(a+b) 3 を展開すると符号は すべてプラス になりす。 マイナスの場合は2番目と4番目の符号がマイナスに! 次にマイナスの展開公式も見ていきましょう。




中学数学 式の展開 因数分解




高校数学 3変数対称式の因数分解 受験の月
3年「式の展開と因数分解」 氏名 ・多項式×単項式多項式の各項に単項式をかける。 例:2x(3x-2y)=6x 2-4xy ・多項式÷単項式多項式の各項を単項式でわる。 例:(6x具体例 冒頭の式の繰り返しになりますが,具体的に三角関数,指数関数,対数関数にマクローリン展開を適用すると以下のようになります。 sin x = ∑ k = 0 ∞ ( − 1) k x 2 k 1 ( 2 k 1)!9/4/17 三次式の展開 今までに、 (xy)2 = x2 2xy y2 ( x y) 2 = x 2 2 x y y 2 などの「2乗の展開」は計算したことがあるでしょう。 3乗ならどうなるでしょうか。 実際に計算してみると、次のようになります。 (xy)3 = (x y)(x y)(x y) = (x y)(x2 2xy y2) = x(x2 2xy y2) y(x2 2xy y2) = x3 3x2y 3xy2 y3 ( x y) 3 = ( x y) ( x y) ( x y) = ( x y) ( x 2 2 x y y 2)
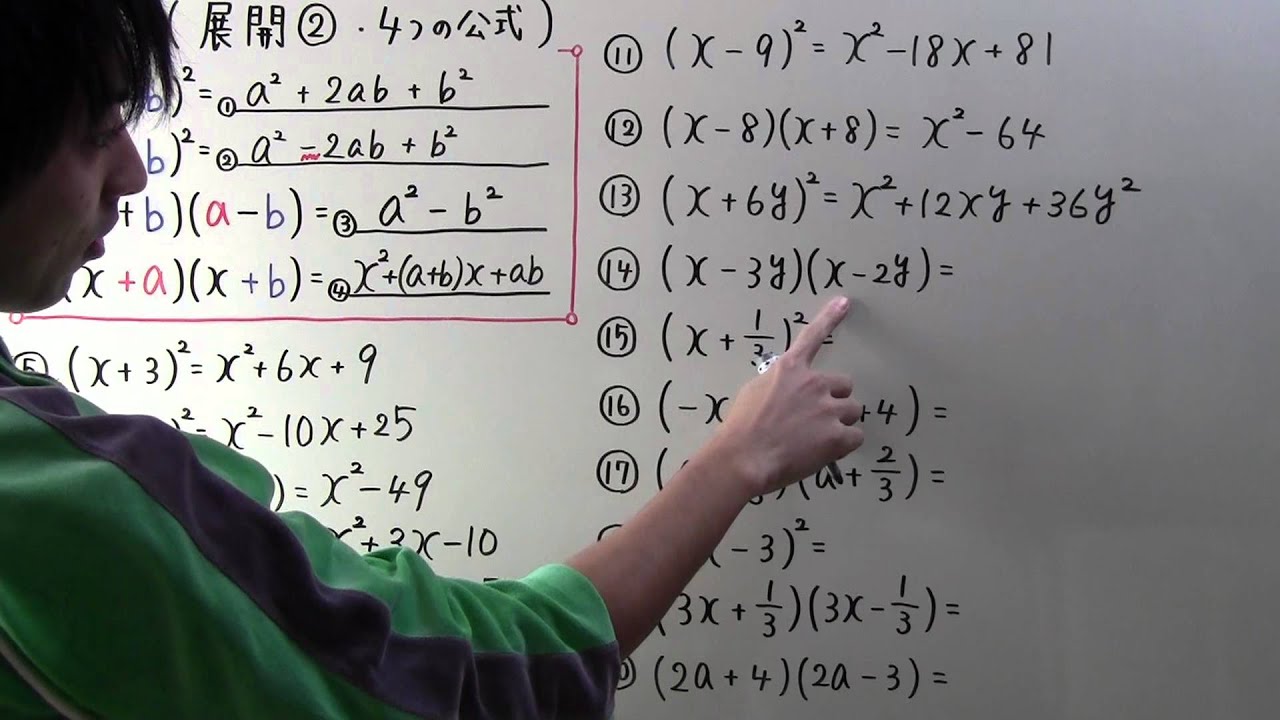



数学 中3 3 展開 4つの公式 Youtube




3乗の因数分解 展開 公式 理系ラボ
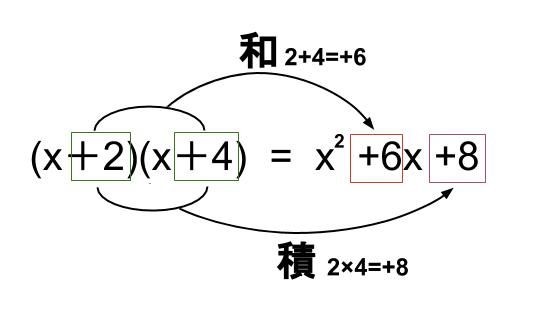
テイラー展開の可能性 ある関数がテイラー展開が可能か否かは,剰余項 R_ {n1} が 0 に収束するかで決まり,剰余項 R_ {n1} が 0 に収束するかは,区間 I の点 x によって異なります. 例として, \mathbb {R}\setminus\ {1\} で定義された関数 f (x)=\frac {1} {1x} の点 0和と差の積 覚え方を紹介していこう! (xa)(xb)の展開公式の覚え方 まず1つめの、16/5/19 中3数学、式の展開の公式・やり方についてわかりやすく説明しました 投稿日:19年5月16日 更新日:年5月7日 中間試験も終わってテストも返ってきたと思います。 結果はいかがだったでしょうか? 今回は、ちょうど試験範囲になった、中3数学の式の
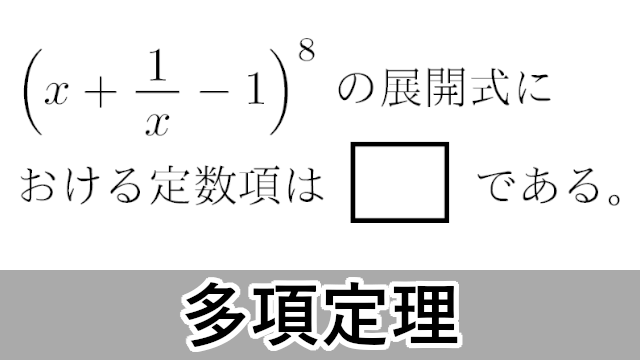



数学 B 多項定理 展開式の係数と定数項 北里大 愛知医科大 福岡大 大学入試数学の考え方と解法
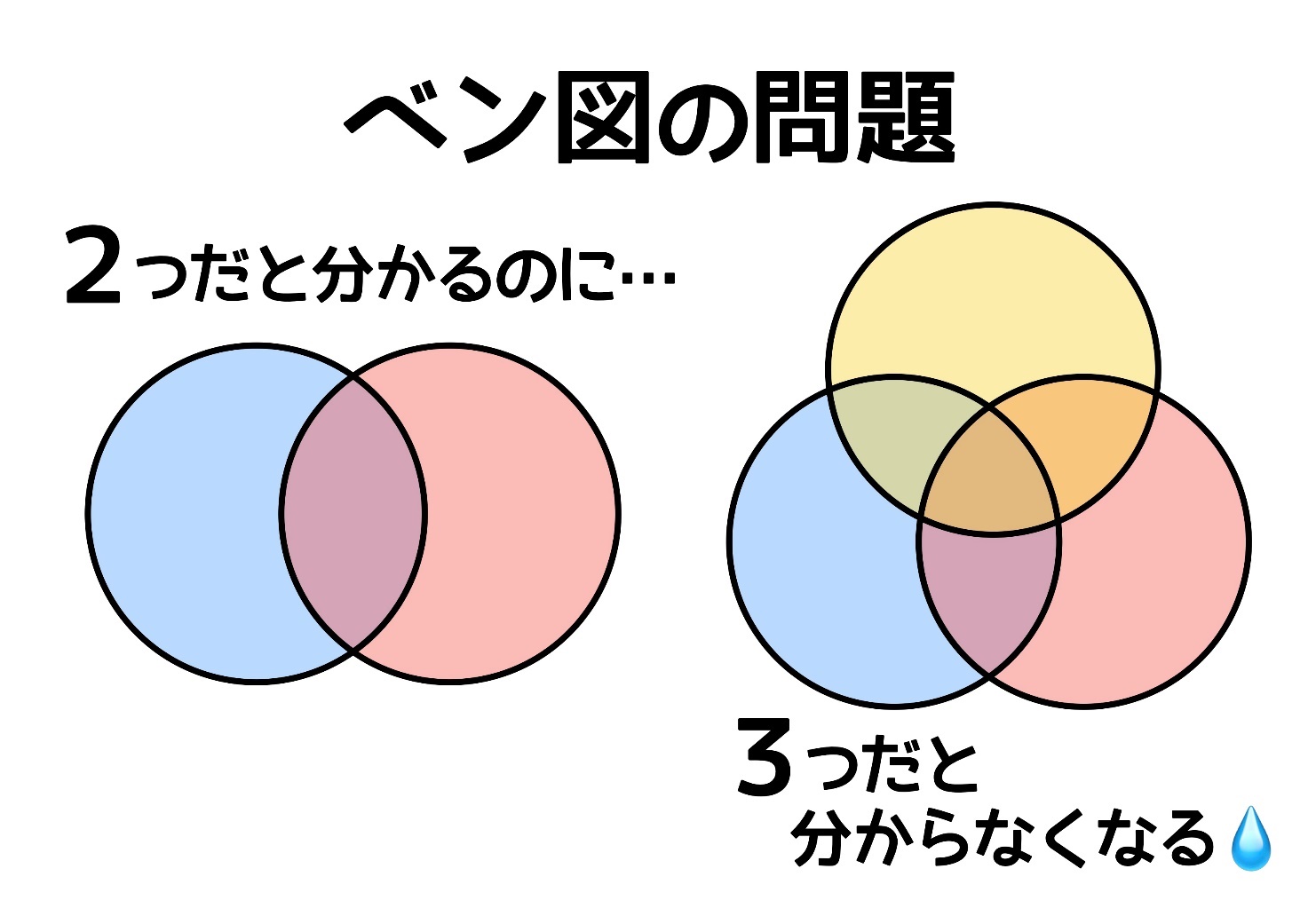



3つのベン図でも慌てない ダブルカウントの理解であっさり解ける 中学受験ナビ
1講 3次式の展開と因数分解(1節 式と計算) 問題集1章 式と証明です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!− 12 − 数学I 2 式の展開 例題 次の式を展開しなさい。 (3a+2) 解 説 まず,( )の中を項に区切りましょう。 3(a +2) 3を( )の中に分配し= x − x 3 6 ⋯ \sin x\\= {\displaystyle\sum_ {k=0}^ {\infty}} (1)^k\dfrac {x^ {2k1}} { (2k1)!}\\=x\dfrac {x^3} {6}\cdots sinx = k=0∑∞ (−1)k (2k 1)!x2k1




中学数学 多項式 の教え方 展開の応用問題




高校数学 A B C 2の公式 映像授業のtry It トライイット
/4/17 単元 多項式の計算, 「乗法公式についてまとめました」, 学年 中学3年生, キーワード 乗法公式,展開25/8/ 3次式の展開公式と練習問題 \(\,3\,\)次の展開公式で覚えておくのは大きく分けると2つだけです。 3次式の展開公式 \(①\hspace{4pt}(ab)^3=a^33a^2b3ab^2b^3\) \(②\hspace{4pt}(ab)(a^2abb^2)=a^3b^3\)動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




乗法公式の問題 a b a b の展開を練習しよう 中学や高校の数学の計算問題




中学3年数学 3項式の展開 Youtube
17/7/21 3次式の展開 (指数法則を利用) (乗法公式を利用) (分配法則を利用) (同類項を整理) ( a b) 3 = ( a b) ( a b) 2 (指数法則を利用) = ( a b) ( a 2 2 a b b 2 ) (乗法公式を利用) = a 3 2 a 2 b a b 2 a 2 b 2 a b 2 b 3 (分配法則を利用) = a 3 3 a 2 b 3 a b 2 b 3 (同類項を整理) このように指数法則や乗法公式を利用すれば、3次式を展開することができ3乗の展開公式に代入しながら計算していきましょう。 (a±b)^ {3}の展開公式 (ab)^ {3}=a^ {3}3a^ {2}b3ab^ {2}b^ {3} (ab)^ {3}=a^ {3}3a^ {2}b3ab^ {2}b^ {3} (x3)^ {3} =x^ {3}3x^ {2}\times {3}3x\times {3^ {2}}3^ {3} =x^ {3}9x^ {2}27x27(3) 長方形EGJIの面積を a, b で表しましょう ・IJ = DH = a(ba) = ID ・EI = FCID = (ba){a(ba)} = baaba = 3a2b ∴ 長方形EGJI = (2ab)(3a2b) → (1)、(2)、(3) ともに「展開」した形でも、解としてOK正解ですね




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく
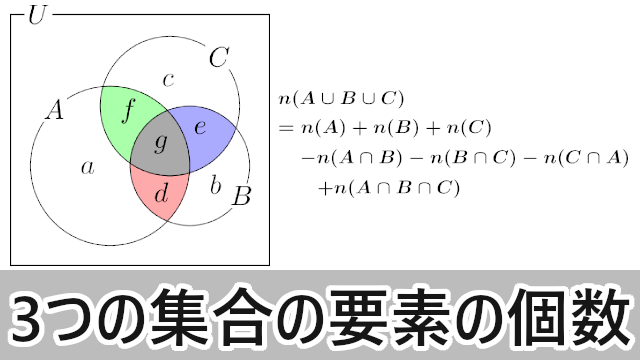



数学ia 3つの集合の要素の個数 大学入試数学の考え方と解法
9/2/03 行列式の展開 定義から2次の行列式ならすぐに求めることができますが, 3次以上の場合にはそうもいきません. そこで,3次以上の行列式を2次以下に展開する方法があります. それは小行列式展開と呼ばれる方法です.たとえば,つぎのように展開でき
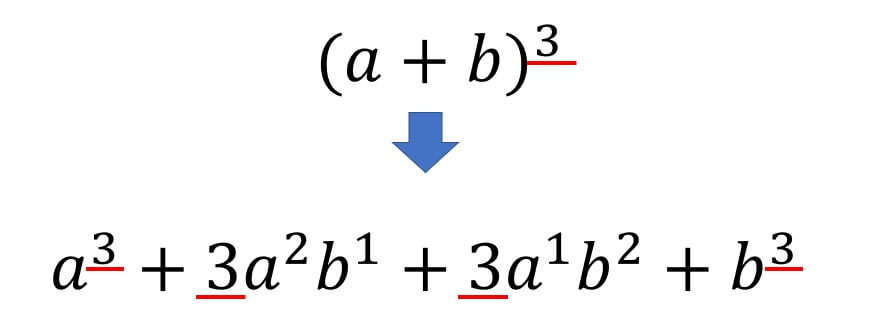



三乗の公式 A B 3乗の展開公式と覚え方を解説




簡単証明 乗法の公式はなぜ使えるんだろう Qikeru 学びを楽しくわかりやすく




高校数学 多項定理 A B C Nの展開式の係数 受験の月




式の展開です かっこの中に3つ数字と文字と入ってるんですよ 答えの解説読んでもいまい Clear
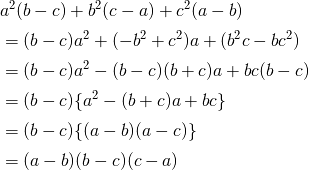



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局
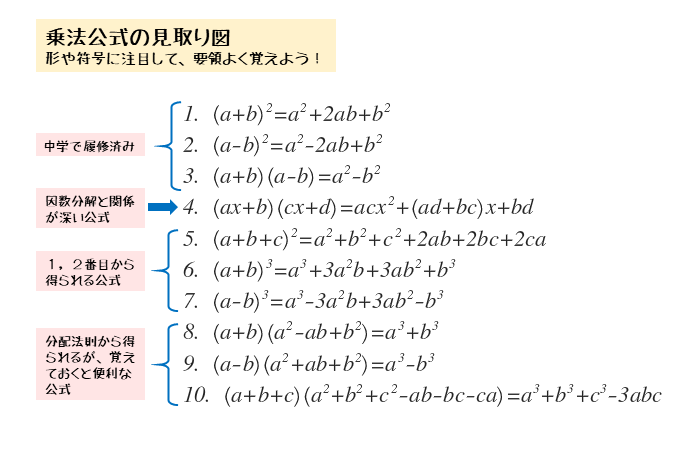



数と式 整式の因数分解について 日々是鍛錬 ひびこれたんれん




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト



必修 4 10 多項式の項の個数と二項定理 わかりmath




因数分解を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
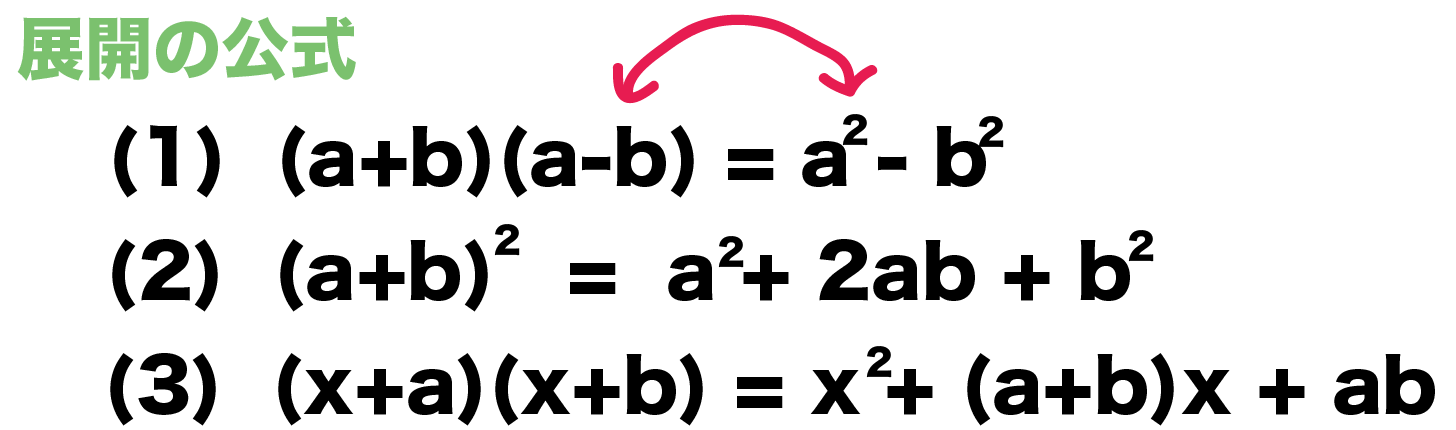



中学数学 因数分解の2つの公式の覚え方 Qikeru 学びを楽しくわかりやすく
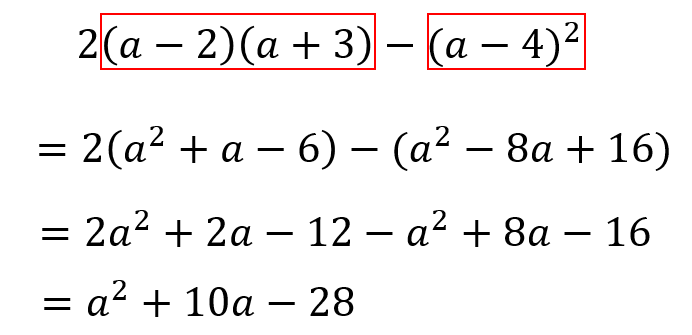



中3数学 複雑な式の展開をマスターしよう 数スタ




展開の公式 乗法公式 の計算方法を図にしてみました あんず学習塾のメモ 図表置き場




板書 展開例でよくわかる 数学的活動でつくる365日の全授業 中学校数学 2年上 永田 潤一郎 永田 潤一郎 本 通販 Amazon
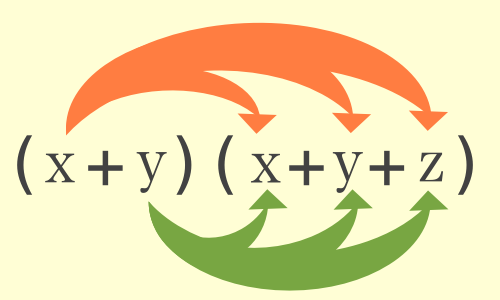



式の展開 簡単に計算できる電卓サイト




基礎編 数学の 式の展開 でつまずいたらココを見直そう まなビタミン




五番の問題です 解説の 3つあるうちの二つ目から意味が分かりません Clear




中学数学 多項式 の教え方 展開の応用問題




中学3年 数学の世界3 多項式の計算と式の展開 教科書予習復習練習問題 赤城 ᐡᐤᐡ
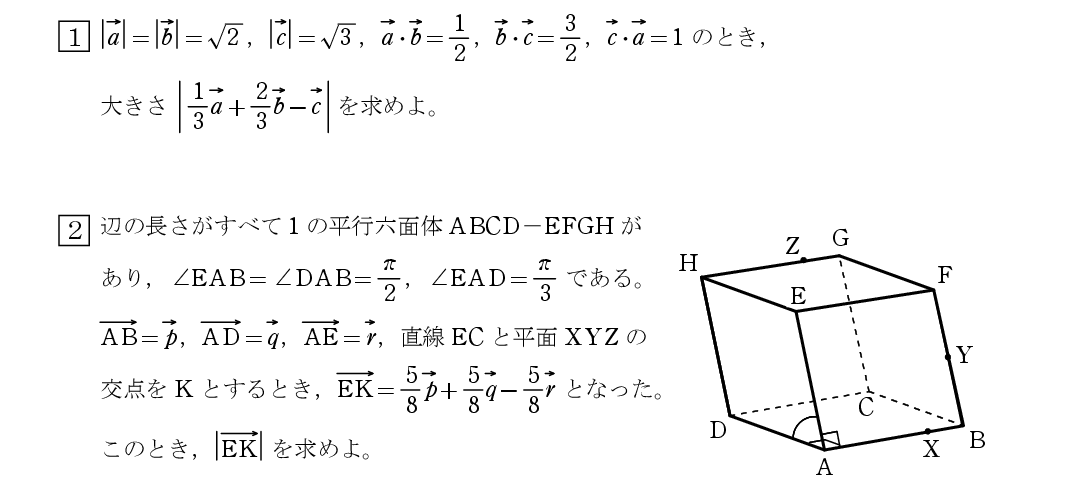



ベクトル 15 空間ベクトルの大きさ計算 怜悧玲瓏 高校数学を天空から俯瞰する




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




展開の公式 乗法公式 の計算方法を図にしてみました あんず学習塾のメモ 図表置き場




式の展開 展開の乗法公式 X A X A の形の解き方とは 中学数学をはじめから分かりやすく




高校数学 数 第1章 数と式 12 文字が3種類ある3乗の公式 壱のblog




文字が3つの因数分解 すうがくのいえ




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




展開 と 因数分解 の4つの基本公式




二項定理を簡単に覚える 定数項 係数の求め方 高校数学の知識庫




部分分数分解の主要パターン おいしい数学




高校数学 数 7 展開 3次式の公式編 Youtube




中3数学 展開とは 練習編 映像授業のtry It トライイット



括弧が3つ以上ある乗法公式を展開するとき 括弧を並び替えてもよいのですか Yahoo 知恵袋




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す



数と式の問題 Of 京極一樹の数学塾会員頁




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




高校数学 展開の工夫 共通部分の置き換え 受験の月




A B C 3の展開も考え方を変えると楽に速く展開できます 大学入試数学の考え方と解法



数学の展開でかっこが3つ以上ある時はどうやって計算するんですか Yahoo 知恵袋




中学数学 多項式 の教え方 展開の基本




数学 2x 3 の5乗を展開せよ の解き方 覚える事は3つだけ てばなすブログ




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく



1



Studydoctor3項式の展開 中3数学 Studydoctor




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su




高1 1 9 数学 かっこが3つ以上の展開 Youtube




乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん



3




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく




中3数学 式の展開の公式 やり方についてわかりやすく説明しました 都立高校受験応援ブログ




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ



数学 2x 3 の5乗を展開せよ の解き方 覚える事は3つだけ てばなすブログ
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな




中3数学 式の展開 因数分解がスラスラ解ける 魔法の授業 学校 塾 家庭教師の1カ月分が1本の動画に On Vimeo




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




基礎編 数学の 式の展開 でつまずいたらココを見直そう まなビタミン



数と式の問題 京極一樹の数学塾
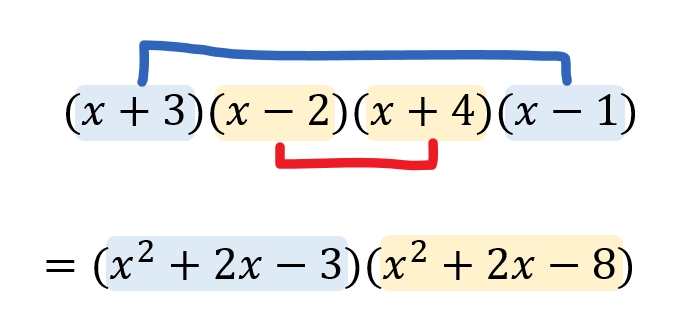



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ



X 2 X 1 1 上の式を展開すると X 2 Yahoo 知恵袋




中学数学 多項式 の教え方 展開の応用問題




中学3年数学 3項式の展開 Youtube




3乗の因数分解 展開 公式 理系ラボ



二項定理について教えてください次の式を中学校の展開で習ったよう Yahoo 知恵袋




基本 三次式の展開 なかけんの数学ノート




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ




中学数学 式の展開 因数分解




文字が3つの因数分解 すうがくのいえ



置き換えによる展開
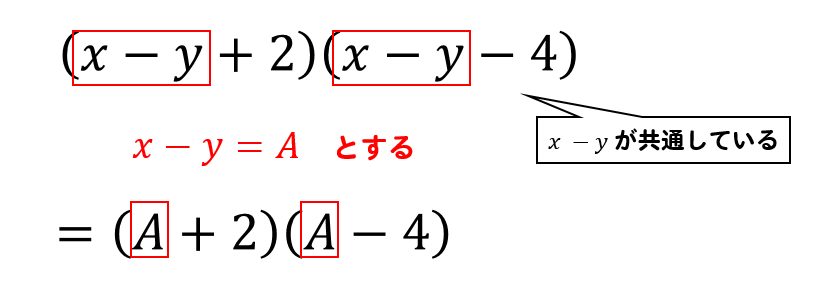



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ
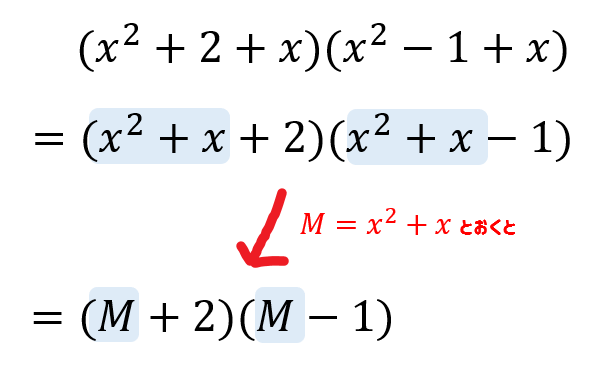



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ



展開公式とは 1分でわかる意味 二乗 3乗の公式 覚え方 問題
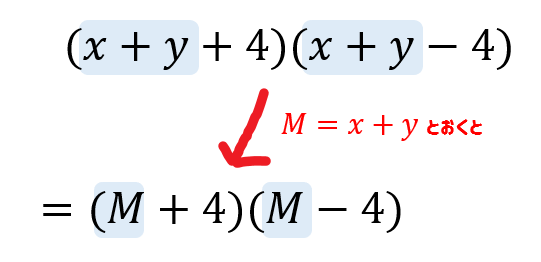



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ




乗法公式 無料で使える中学学習プリント



4月22日更新 中3一斉授業 数学 展開 乗法公式 担当 中嶋 成績 上がってます 根城学習塾 八戸市




中3数学で習う展開公式 齋藤 皓正オンライン家庭教師のブログ マナリンク




3乗の公式 文字3つ 超わかる 高校数学 A 授業 展開 因数分解 21 Youtube




世界一わかりやすい数学問題集中1 1章 正の数 負の数




高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト



Q Tbn And9gctvyxsiane6xsfgba5 Aeuwoo0bsffzdws04eudn0eg3sgi5vzu Usqp Cau




乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語
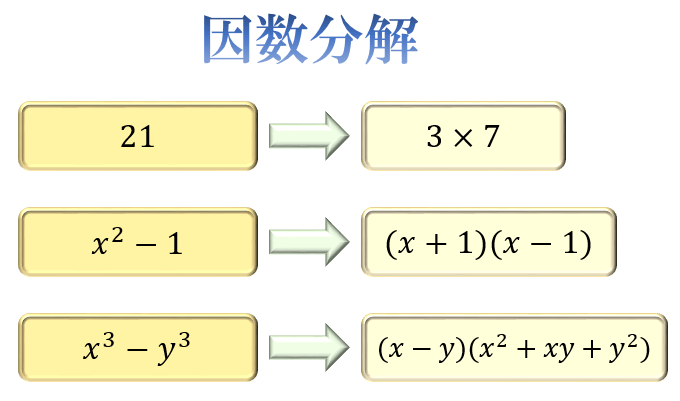



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




高校数学 2次3項式ax Bx Cの因数分解 たすき掛け 受験の月
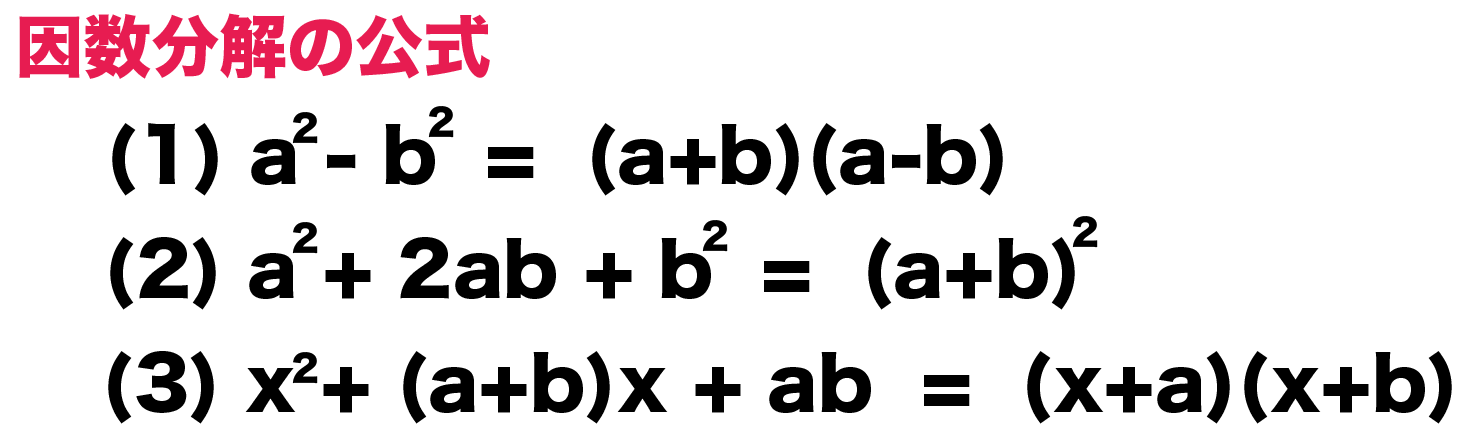



中学数学 因数分解の2つの公式の覚え方 Qikeru 学びを楽しくわかりやすく



1




S計算 部分分数分解編 おいしい数学




3つ項の式の展開 Youtube




高校数学 3変数対称式の値 X Y Z X Y Z など 受験の月



0 件のコメント:
コメントを投稿