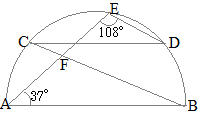
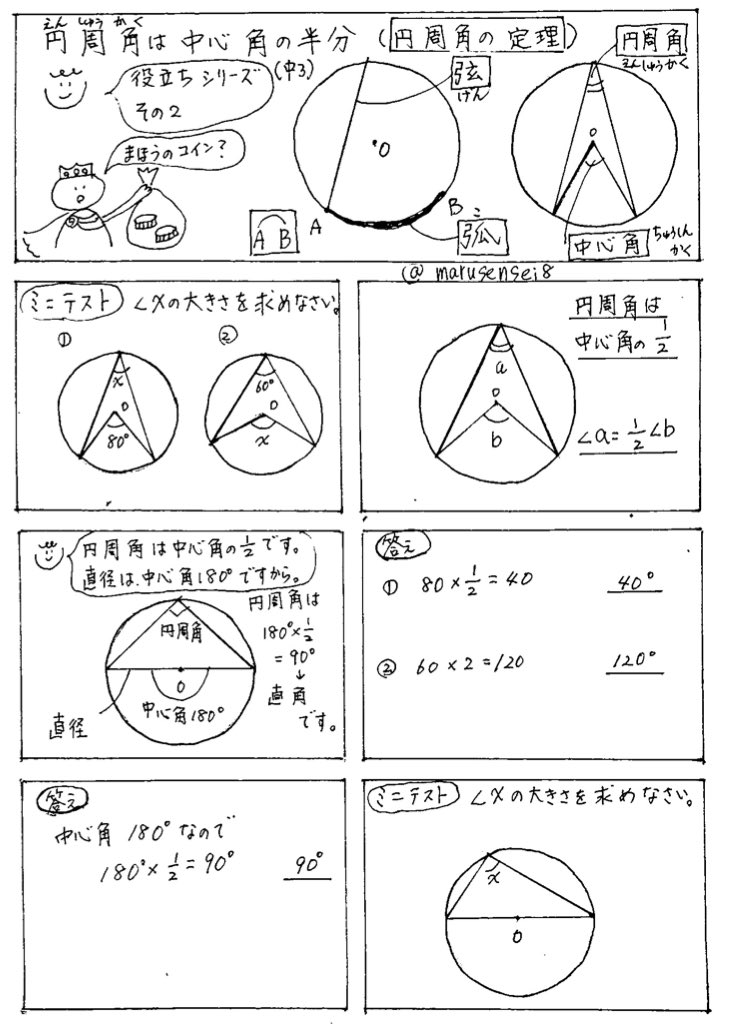
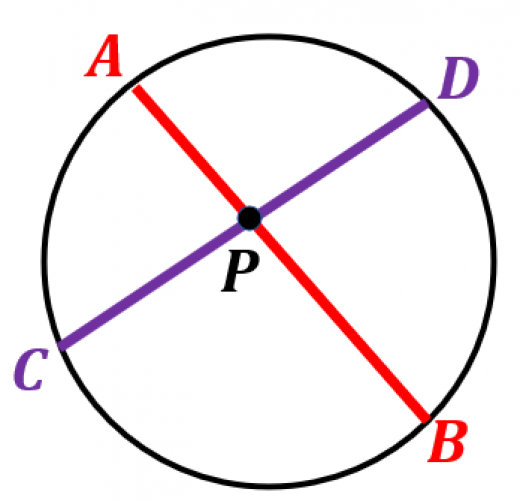
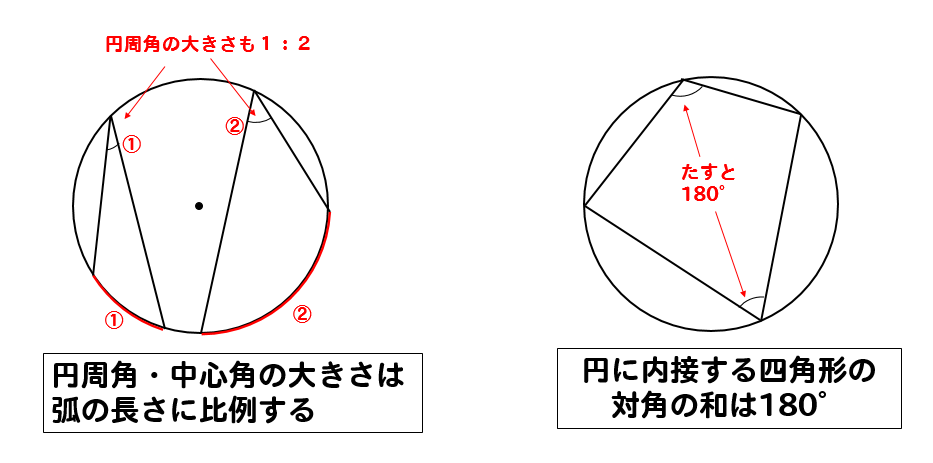
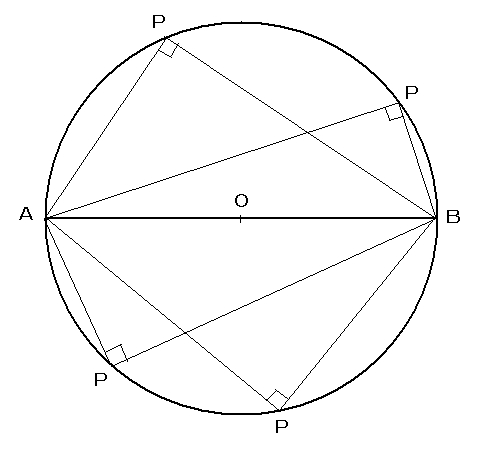
円周角の定理 (入試問題) → 携帯版は別頁 弧(こ)・弦(げん)とは 円周の一部を「弧」という. 例 右図の赤で示した部分を 弧 AB などという.(これに対して灰色で示した線分は 弦 AB という.) ※ 1つの弦により円周全体は2つの弧に分けられる円周角と中心角(3) 1 半円の弧に対する円周角は90°である。 (グーレスの定理) P A B (1) (2) 次の図で、∠xの大きさを求めなさい。 363 x 65° x (3) (4) (5) 32° x 65° O x (6) 67° x 40° O 23° 50° 58° 25° 25° ・ ・ ・ ・ ・ ・ O O O A B 円周角の定理の逆を使った相似の例 さきほどの続きで直線ACと、直線BDの交点をEと置きます すると、 AEDと BECについて相似を示すことができます。 円周角の定理が使えると、対頂角と合わせることで、簡単に相似は証明できます。
平面幾何 京極一樹の数学塾
円周角の定理 問題 難問
円周角の定理 問題 難問- c,e,p,fは同一円の円周上の点でした(円周角の定理の逆) →これは書いてから直ぐに気がつきました。失礼しました。 bcfが2等辺3角形になるんですね。 (弧ecの円周角が°だからf=30=50°) 後は全てokです。 これなら中学生が解ける図形問題として納得です。弧bcに円周角を考えると円周角は中心角の半分のため∠bac=44度。 今問題文の条件から⊿abcは二等辺三角形のため底角は等しい。つまり∠abc=∠acb=(180-44)/2=68度 求めたいと思っていた∠bcd=∠acb=68度 ⊿bdcに注目すると∠bdc=180-68-46=66度となる。



円周角の定理 入試問題
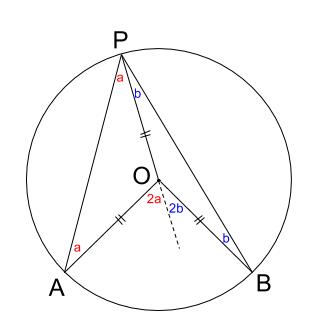
円周角の定理は 「円周角=½ 中心角」ですから、 ∠bac=½ ∠boc を示せばいいわけです。 oからbに補助線を引いて、大きさが同じ角に印をつけてみましょう。 注意すべきなのは、oは円の中心であり、a,b円周上の点であるため、oa=obであることです。難関私立高校対策 シンプル難問 難関私立高校対策 シンプル難問 ※新たな視点を学び、解決の幅を広げる良問を扱います。 シンプルに見えて手ごわい問題です。 (1)35x+32y=15を満たす (2)次の円の面積を求めなさい。 自然数x、yをすべて求めなさい。 (3)図の四角に当てはまる長さを求めなさい。 (4)円の半径を求めなさい。 ~1~数学36章 円の性質「円周角と中心角」<基本問題・解答> 解説 (1)円周角は中心角の半分なので (3)中心角は円周角の2倍なので (4)右の図のように、線分aoを引き二等辺三角形を 2つ作る。 c 二等辺三角形の底角は等しいので〇=° =45°
円周角の定理「 1 つの弧に対する円周角は一定」 を利用して, 角度が等しいときにその 2 つの角をつくる 4 点が同一円周上にある ことを証明していきます。 円周角の定理の逆は, 2 点 , が直線 について同じ側にあるときに が成り立つならば, 4 点 , , , は1つの円周上にある。 こんにちは! スマホ1台でマンツーマン指導を受講できる、数学専門オンライン塾の数強塾です。 ★本日も算数・数学に関する動画を更新しました! 慶應義塾女子高校入試問題|円周角の定理難問 慶應義塾女子高校入試問題の難問です。円周角の定理の基本 名前 次の()にあてはまる言葉を書きなさい。 ①1つの弧に対する円周角の大きさは( )。円周角は、 その弧に対する( )の半分である。 下の図で角xの大きさを求めなさい。 ① ② x ° ° ③ ④ ° x ° ⑤ ⑥ 1 2 48 1 105 114 NO 1 /8点 x o o x
難問10(灘高校) 今回の問題は、二等辺三角形の性質や円周角の定理等を使えるかがポイントです。同じ大きさの角や90°をうまく使えるかにかかっています。頑張って下さい! 問題10 解答10 円周角と三平方トレミーの定理が背景? 高校入試 数学 良問・難問 円周角と三平方トレミーの定理が背景? 中学校の定期テストは,基本的にどの先生も出す問題は同じです。 出題の仕方で個性が出たりしますが,基本的にはその先生の授業をしっかり聞いて,対策すれば点は取れるもの。 たまに平均点30点台とか,かなりテストの作り方間違え円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方の定理の証明(3) 三平方の定理(1




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室
こんにちは!レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 見た目はシンプルで一見簡単そうに見えますが、かなりの難易度だと思います。 さすが灘 (*´Д`) ヒント 答え 詳しい解説 ①補助線を引く ②abの長さを求める ②1 相似を見つける ②2 de ea = bd ba ③三平方の円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 2つの半径OA, OBと弦ABによって できる三角形は必ず二等辺三角形になる。 A B O 中心Oに向かって補助線をひき、二等辺三角形や中心角をつくる。 A,B,C,Dが円周上の点のとき、∠xの値を求めよ。 36° 32° x A B C O O A B C D 58° x A B C D O 30° 130° x場面を取り上げることはほぼないと感じる。そこで円周角の定理を用いた証明問題を取 り上げる。本論文は,その教材及び実践内容,それに対する考察を報告するものである。 <キーワード>円周角,三角形の外角の性質,図形,証明,サッカー 1.はじめに




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
円周角の定理に関する基本的な問題です。基本事項下の図のように 一つの孤に対する「円周角」の大きさは,「中心角」の半分になります. 同じ弧に対する円周角は等しくなります。覚えるのはこの2点だけです。 このような形になっている場合も円周角は中心角の半分になります。円周角の定理とは (1)(2)円周角の定理 基本問題解説! (3)(4)見た目がややこしい 問題解説! (5)(6)直径に対する円周角、弧の長さ等しい問題解説! (7)(8)弧の長さと比に関する円周角の問題解説! (9)(10)内接する四角形、接線に関する問題解説! 円周角の問題まとめ① また、角dae=角dceより、円周角の定理の逆から、四角形acdeは同一円周上にある。② ①②より、5点abcdeは同一円周上にある。 よって、孤abに対する円周角について、 角aeb=角adb つまり、今問題で問われている角cad角aebは角cad角adb=角cfdと等しい。
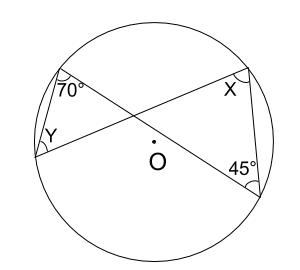



中学数学 円周角の定理 例題その1 中学数学の無料オンライン学習サイトchu Su



至急お願いします 中2の数学です 下の図で 同じ印をつけた角 Yahoo 知恵袋
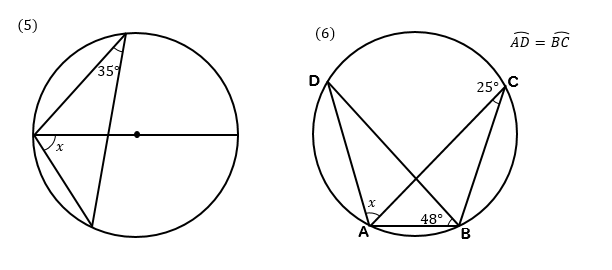
円周角の定理の解説・問題の解き方 三角形・四角形などの角の大きさについてはこれまで扱ってきましたが、ここから円と多角形が組み合わさった、さらに複雑な問題を扱うようになります。 覚えるべき定理はいくつかありますが、最も重要なのが今回解説する『円周角の定理』です。 今回は円周角の定理だけではなく、これに関連した定理を紹介して、問題を入試問題に挑戦! 解答と解説のページ(5) 時習館 ゼミナール・高等部 平成25年度岐阜県 数学 超難問 (正答率0%) 解答と解説 三角形 ABH と 三角形 ACDで、弧ADに対する円周角は等しいので、 角∠ABH = 角∠ACD 問題文より、角∠AHB = 90° 半円の弧に5 円周角の定理の逆 ama06 練習問題へ ③ u cde で,内角と外角の関係より ∠cde =90 °-40 °=50 ° よって,2 点a,d は直線bc について同じ側にあり ∠bac =∠bdc =50 ° ←円周角の定理の逆が成り立つ したがって,4 点a ~d は同じ円周上にある。 ゆえに, ①,③ ①,③(答)




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット
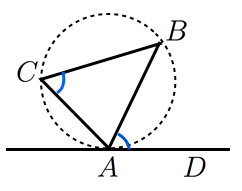



接弦定理とその逆の証明など 高校数学の美しい物語
定理 1 : 1 つの弧に対する円周角は中心角の半分 定理 2 : 1 つの弧に対する円周角はすべて等しい ∠ A Q B = ∠ A P B = ∠ A R B (すべて AB ⌢ に対する円周角) 1:10 例題 10 選 (1) 対頂角は等しい (紫の角) 1 つの弧 (オレンジ色)に対する円周角は等しい 円周角の定理 三平方の定理 相似 角の二等分線と比 比例式 おなじみのメンバーです。 解き方です。 まずは問題文からわかる事を書きました。 見やすいですね(適当) 円周角の定理より 弧ADに対する円周角は等しいので 半円に対する円周角は直角なので円周角1 それぞれのxの値を求めよ。 ただし、点Oは円の中心である。 78° x O x O 56° 49° x O O 62° x x O 132° 6° x O O x 128° 109° x O x 28° x 102° x 18° 24° O ° 30° x ①の解説 ②③④⑤⑨の解説 ⑥⑧の解説 ⑦の解説 ⑩の解説 ⑪の解説 ⑫の解説




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




とある初等幾何の超難問の解法
それを言えるようになるためには「 円周角の定理をパッと言えるようになること 」が必要です。これができる人は円周角の問題で高得点を取ることができます。 皆さんは「円周角の定理を全て説明してください」と言われたらパッと的確に説明できますか? 大阪府の問題は,(えげつないのも多いですが)丁度良い図,難易度の問題も多い気がします。 要素が多すぎて,北海道の入試では出せなさそうだけど,日頃の学習の成果を試すには丁度良い問題。 後半の問題はそのうち追加します。 TITLE:円周角と大量の二等辺1 出典:19年度大阪府C 範囲:中3円周角 enshuNi_1pdf Google Drive Sign in Loading {"id円周角(えんしゅうかく)とは、ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。 円周角 c は 0




図形問題 13 開成高 東久留米 学習塾 塾長ブログ



平面幾何 京極一樹の数学塾
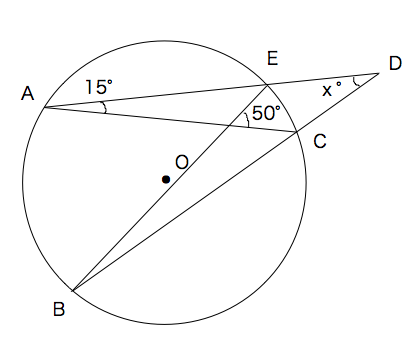
円周角の定理(入試問題) 要点 一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 二等辺三角形の2つの底角は等しい. (2) 円周角は中心角の半分になる. 特に, (1)を使って元の角 x の代わりに,他の角 ∠ BAC で計算する方法が使えるようにしましょうFdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date 4/9/19 PM 単元 円周角の定理(円周角と中心角),円周角の定理の利用, 「数学 超難問 暇な時などにやってみては?」, 学年 中学3年生, キーワード 数学,超難問,kikinote,math



Www Aichi Phsnyuushi Unit Com App Download 80 90 E5 95 8f E9 A1 8c Ef 8b E8 A3 E8 Ac 80 91 E9 9b A3 E9 96 E7 81 E7 Ab 8b E9 Ab 98 E6 A0 A1 E5 Af Be E7 Ad 96 Ef 97 Ab E9 9b A3 E5 95 8f Ef Pdf T




円周角の定理 数学a フリー教材開発コミュニティ Ftext
円周角の問題に 取り組む際に、 次の3つのポイントに注意して 問題を見てみましょう。 ①弧に注目する ②直径が出てきたら 90°の円周角を探す ③補助線を引いてみる それぞれについて 説明を行っていきます。 ①弧に注目する 「円周角の問題だから円の総合問題・その5・相似の利用の難問 問題 下の図のように、円周上に、 \(5\) 点 \(A,B,C,D,E\) があり、\(\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ CD }\) である。 円周角の定理は円の内側で考える問題でよく使われます。 同じ弧からピザが出ていた時は円周角の定理が使えます。 同じ弧を見つけることがポイントです。 補足メモ 同じ弧が別の場所にある問題を応用問題で作りたい。



数学クイズ なん度 Finalstage 全問のヒント 数学クイズ なん度 Math Quiz Find Angles




高校入試 高校入試 数学 良問 難問




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




とある初等幾何の超難問の解法



大人は解けない 超難問 第9回算数オリンピック ファイナル問題より どう解く 中学受験算数




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
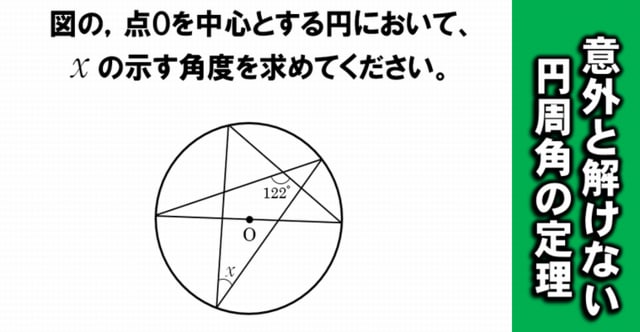



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ




中学数学 円周角 中心角
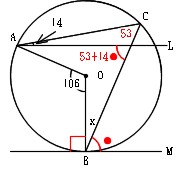



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
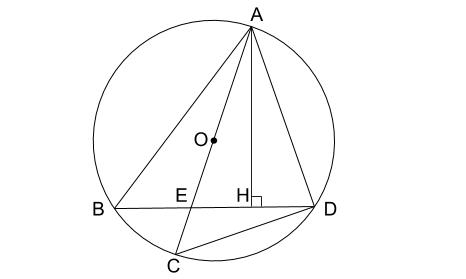



高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su
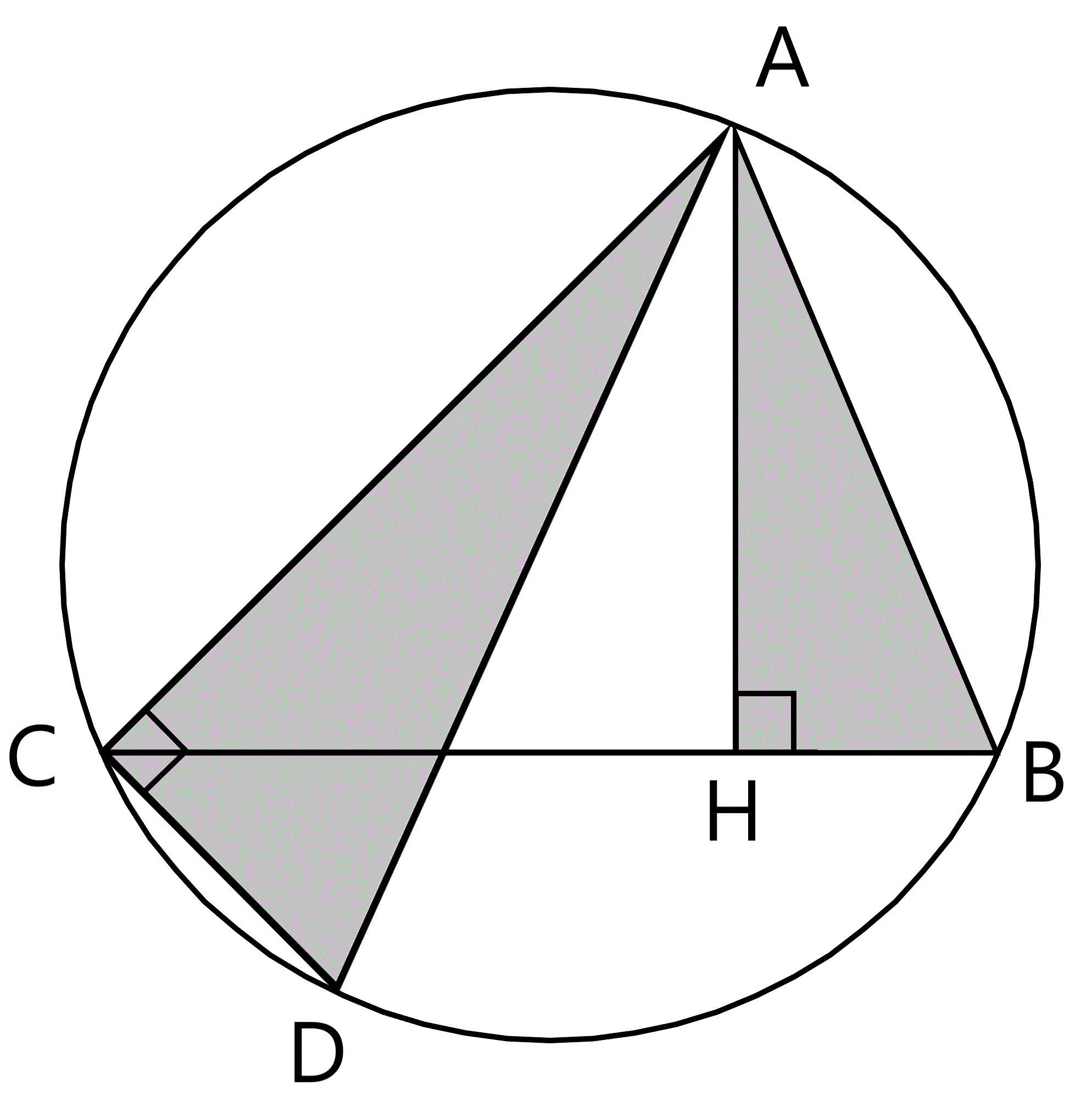



中学数学 外接円の半径の求め方 田中の日記




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube




数学 中3 57 円周角の定理 少し応用編 Youtube



Www Aichi Phsnyuushi Unit Com App Download 80 90 E5 95 8f E9 A1 8c Ef 8b E8 A3 E8 Ac 80 91 E9 9b A3 E9 96 E7 81 E7 Ab 8b E9 Ab 98 E6 A0 A1 E5 Af Be E7 Ad 96 Ef 97 Ab E9 9b A3 E5 95 8f Ef Pdf T




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
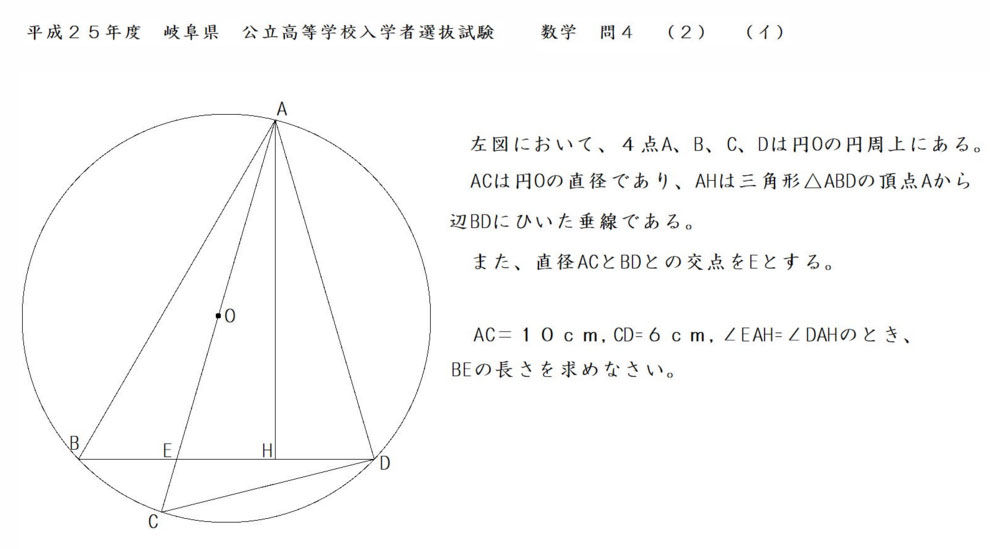



平成25年岐阜県数学4 正解率0 を高校数学で解く 東大合格コム
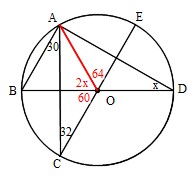



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



Math 円 4 円周角の難しい問題を解くコツ 働きアリ The 2nd



1



高校入試 数学 無料学習プリント教材
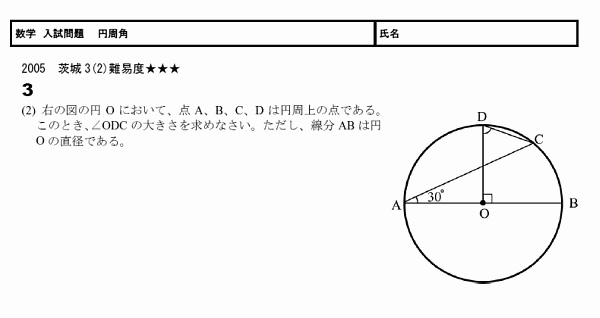



高校入試 数学 無料学習プリント教材



円周角の定理 練習問題 苦手な数学を簡単に
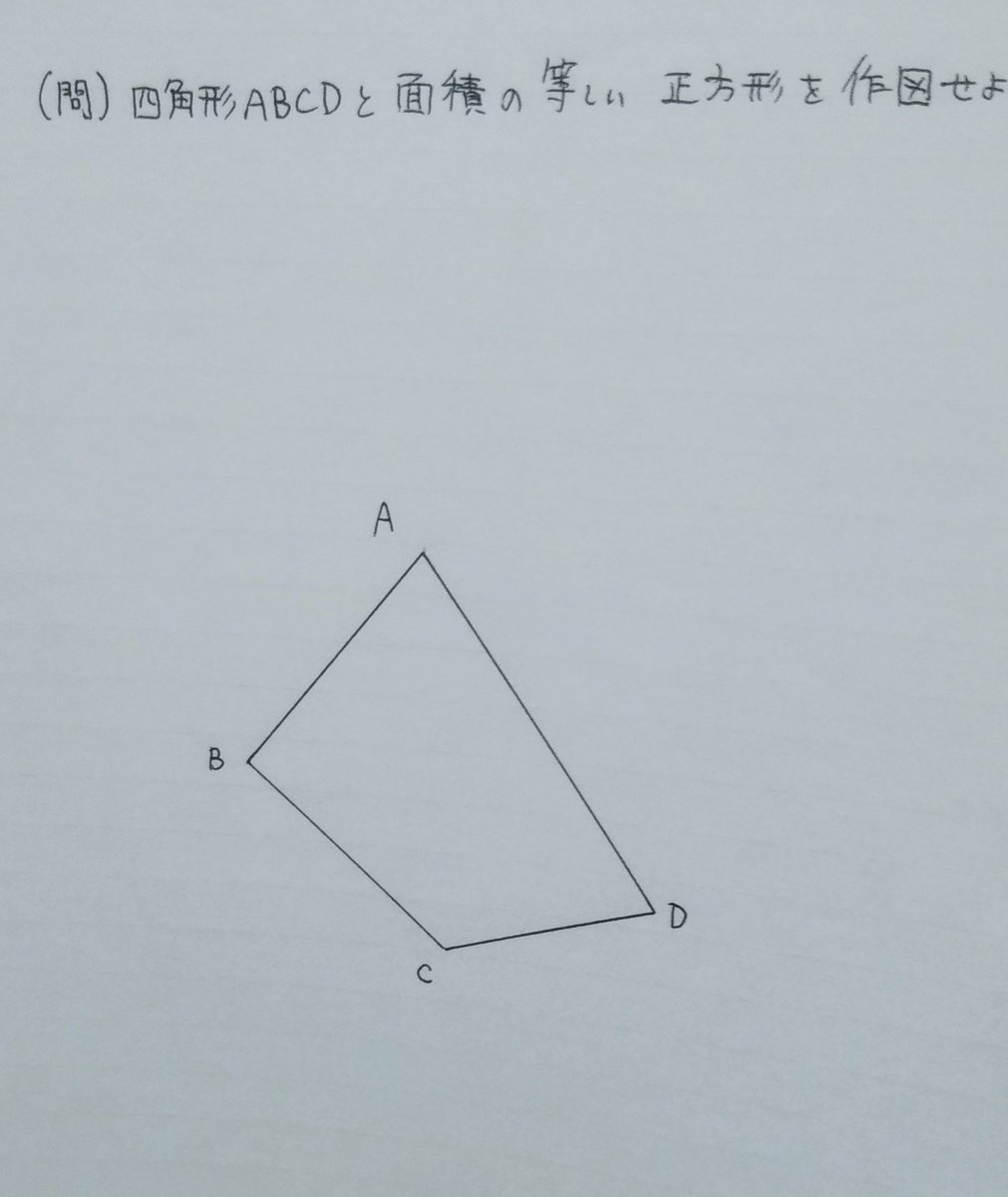



ベリースライム A Twitter 中学数学における作図の最高峰 中3までの知識で作図できます 平方根 2次方程式 相似 円周角 三平方の定理を含むスーパー問題 知っている方も暇つぶしにどうぞ 数学 作図 難問



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス




中学生でも解ける外伝 高校入試難問35 灘高 日比谷高校のススメ



高校入試数学 円と三平方の定理の利用の融合問題




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット



1
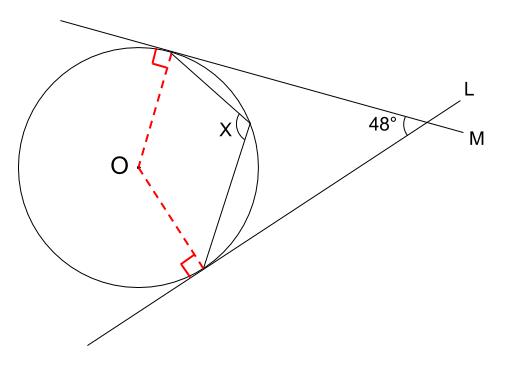



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



1




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット
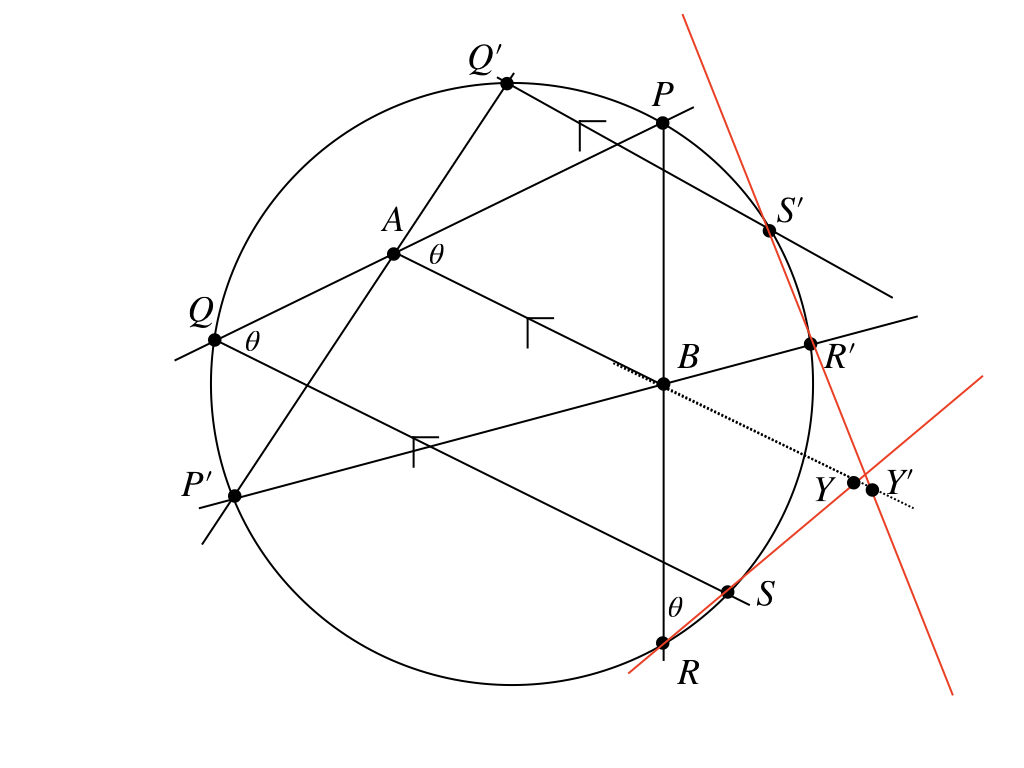



京大の良問に学ぶ平面図形の3つの解法 初等幾何 ベクトル 座標平面 物理u数学の友 質問 悩みに回答します




図形問題 3 灘高 東久留米 学習塾 塾長ブログ
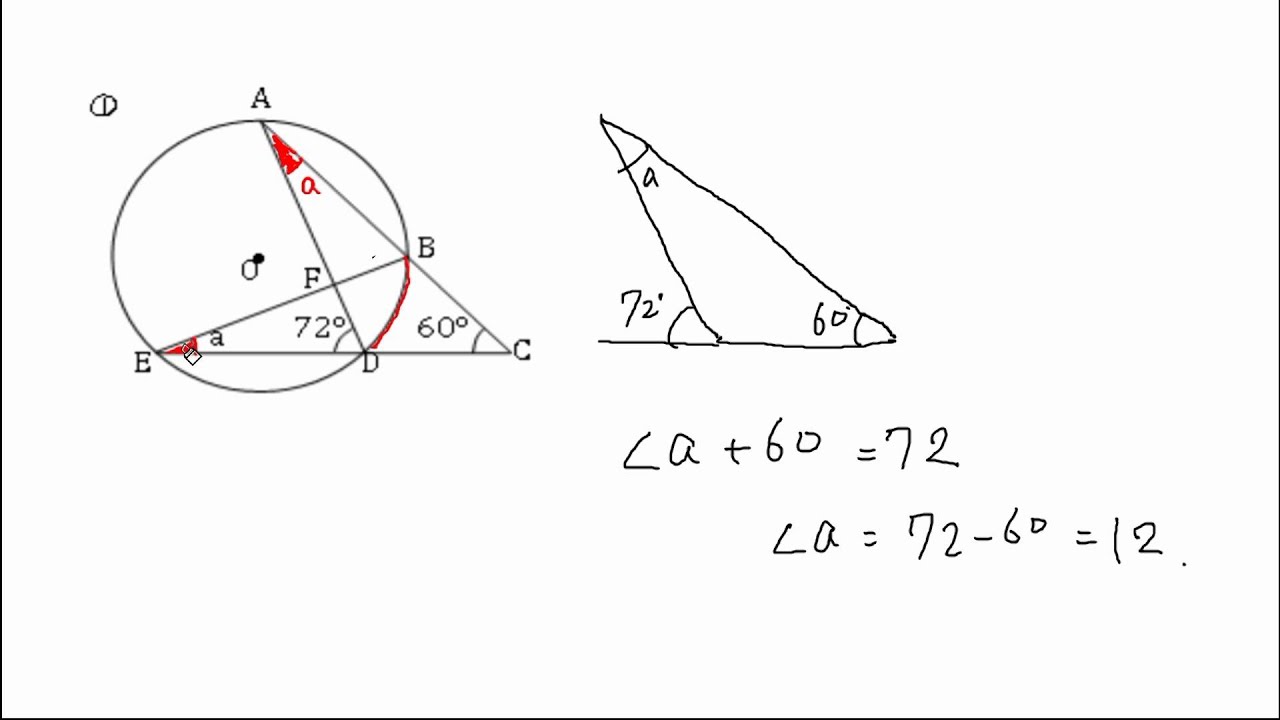



円周角の定理 問題 Youtube
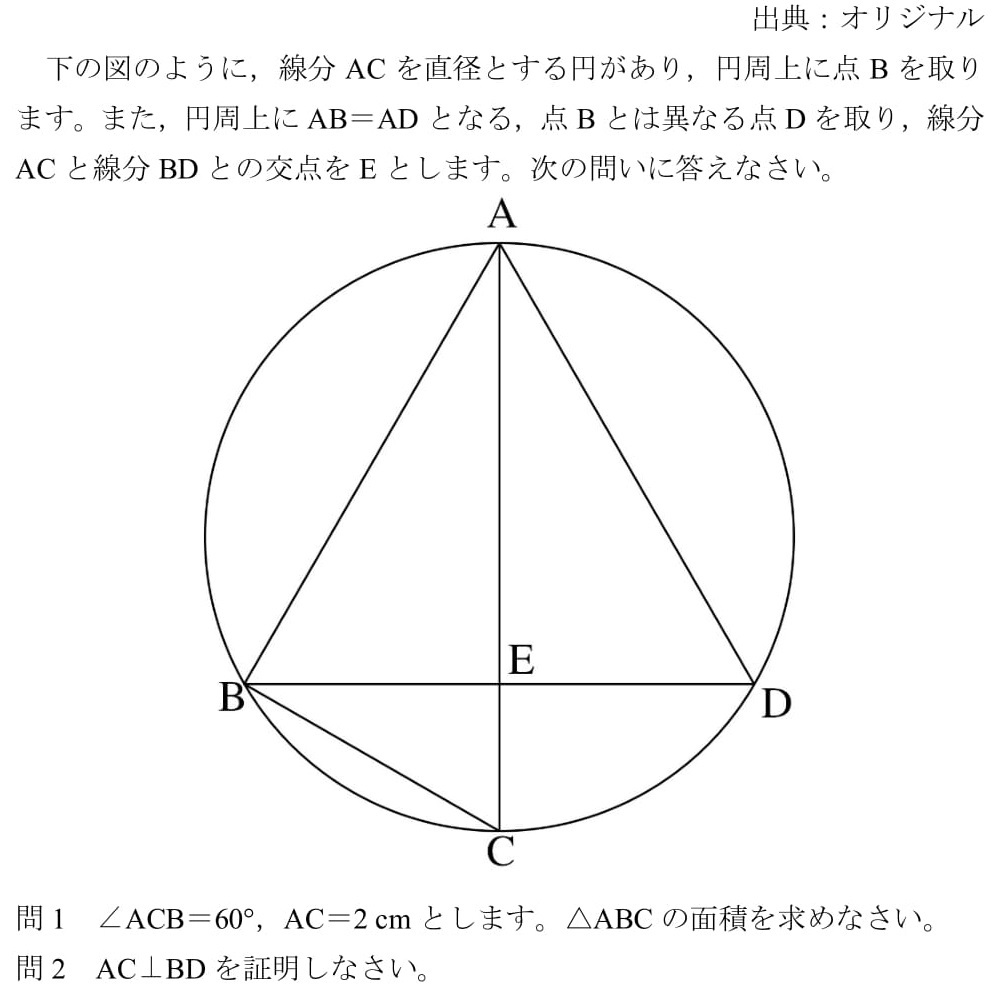



円周角証明の究極系 オリジナル 高校入試 数学 良問 難問
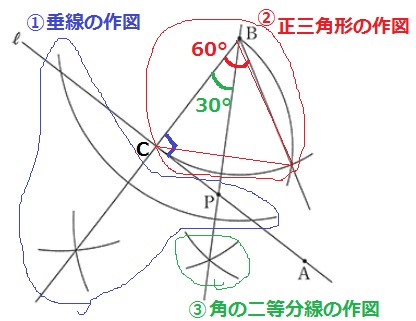



年度 千葉県公立高校過去問 前期 数学 解説 家庭教師サボの部屋
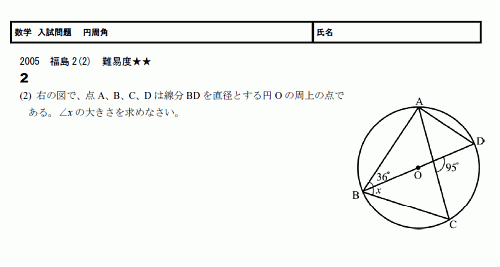



高校入試 数学 無料学習プリント教材



円周角の定理
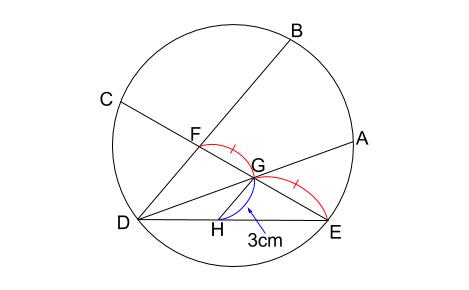



円の総合問題 その5 相似の利用の難問 中学数学の無料オンライン学習サイトchu Su



円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
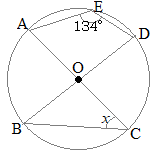



円周角の定理 入試問題




高校数学a 共円条件 4点が同一円周上にある条件 受験の月




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
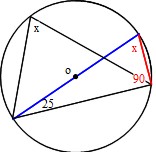



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3 数学 超難問 中学生 数学のノート Clear




30秒で角度を求めよ 円周角の定理 勉強 Youtube スタディチューブ




円周角 補助線を引く問題
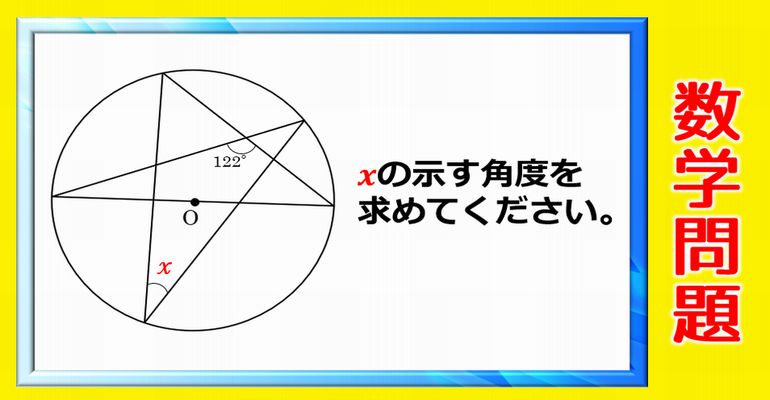



数学問題 大人は意外と悩んでしまう円周角の定理 ネタファクト
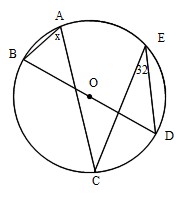



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
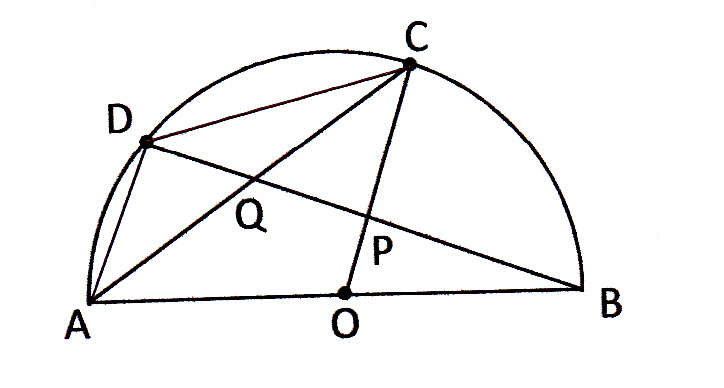



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
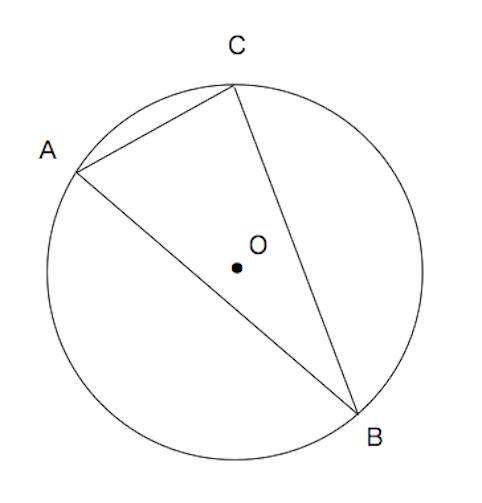



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に



方べきの定理とその統一的な証明 高校数学の美しい物語




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所




ひたすら都内の高校受験の数学の問題を集まるブログ 毎日解くと第一志望に近づくかも しれない たまに学校紹介も 入試問題




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



入試問題に挑戦 平成17年 宮城県 超難 時習館 ゼミナール 高等部




中学生でも解ける外伝 高校入試難問35 灘高 日比谷高校のススメ




接線と弦の作る角 接弦定理 無料で使える中学学習プリント



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




円周角 三角形の外角の関係を使う問題




勉強しよう数学解答集 15



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理 入試問題



パズル攻略 数学アプリ なん度 Finalstage 8 の解法 分かりやすい解説 Kenpiの灰色マインドマップ日記



円周角の定理は中学何年生でならいますか 学習指導要領が変わったので 中 Yahoo 知恵袋



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所



中学数学 高校入試で使える重要公式を一覧でまとめておくよ 数スタ



例題対比 円周角の定理
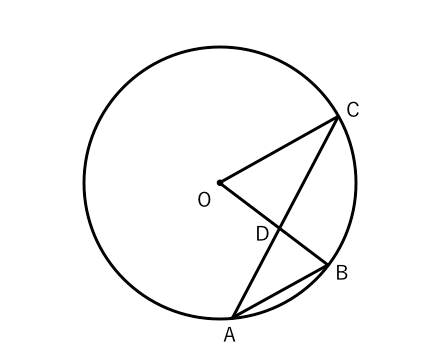



毎日問題を解こう 7 苦手な数学を簡単に
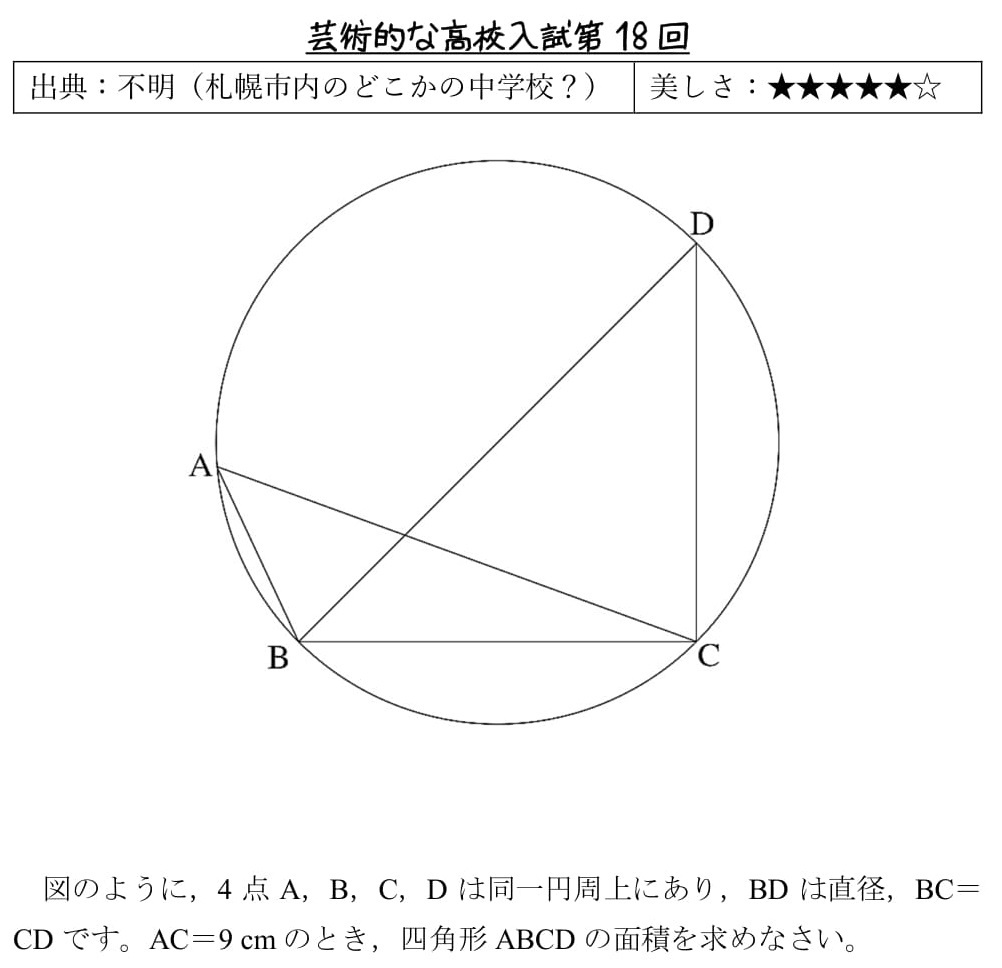



円周角と三平方 トレミーの定理が背景 高校入試 数学 良問 難問




中3 数学 超難問 中学生 数学のノート Clear




中学数学発展 三平方の定理の良難問 灘高校過去問 定期テストや高校入試に レオンの中学数学探検所




円周角の定理を使わずに解け 中学受験 算数 数学 難問 小学生 中学生 Youtube
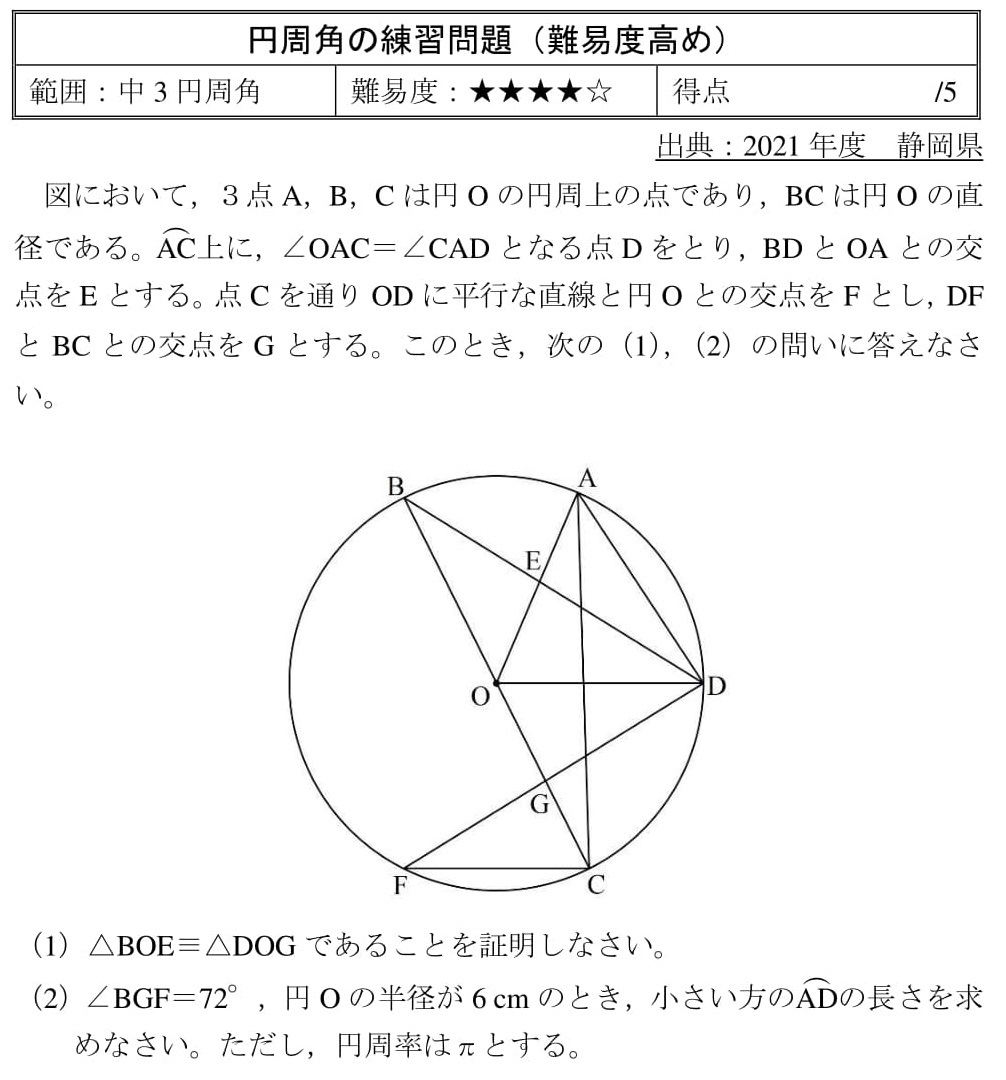



高校入試 数学 良問 難問
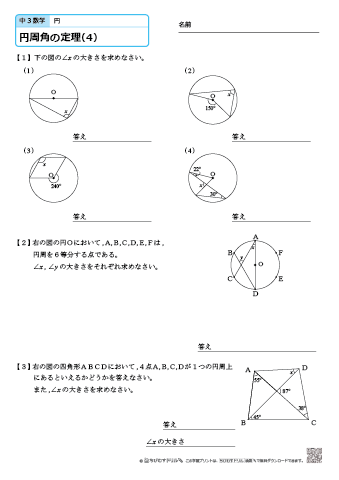



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
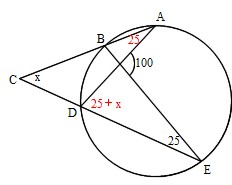



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
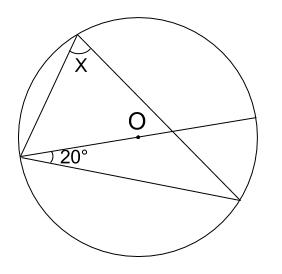



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su




数学 中3 超難関問題 問題を写真に載っけておきました 相似や円周角系や Okwave
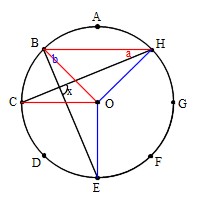



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



1



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス
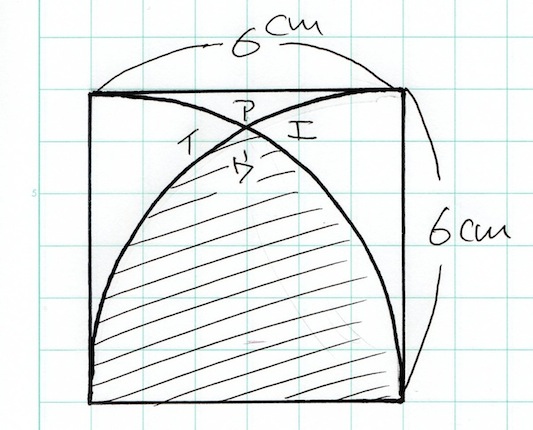



超難問 ねこたさんのごった煮日和



円周角の定理と中心角 中学3年数学 Youtube
.png)



中学数学の問題を解くコツ
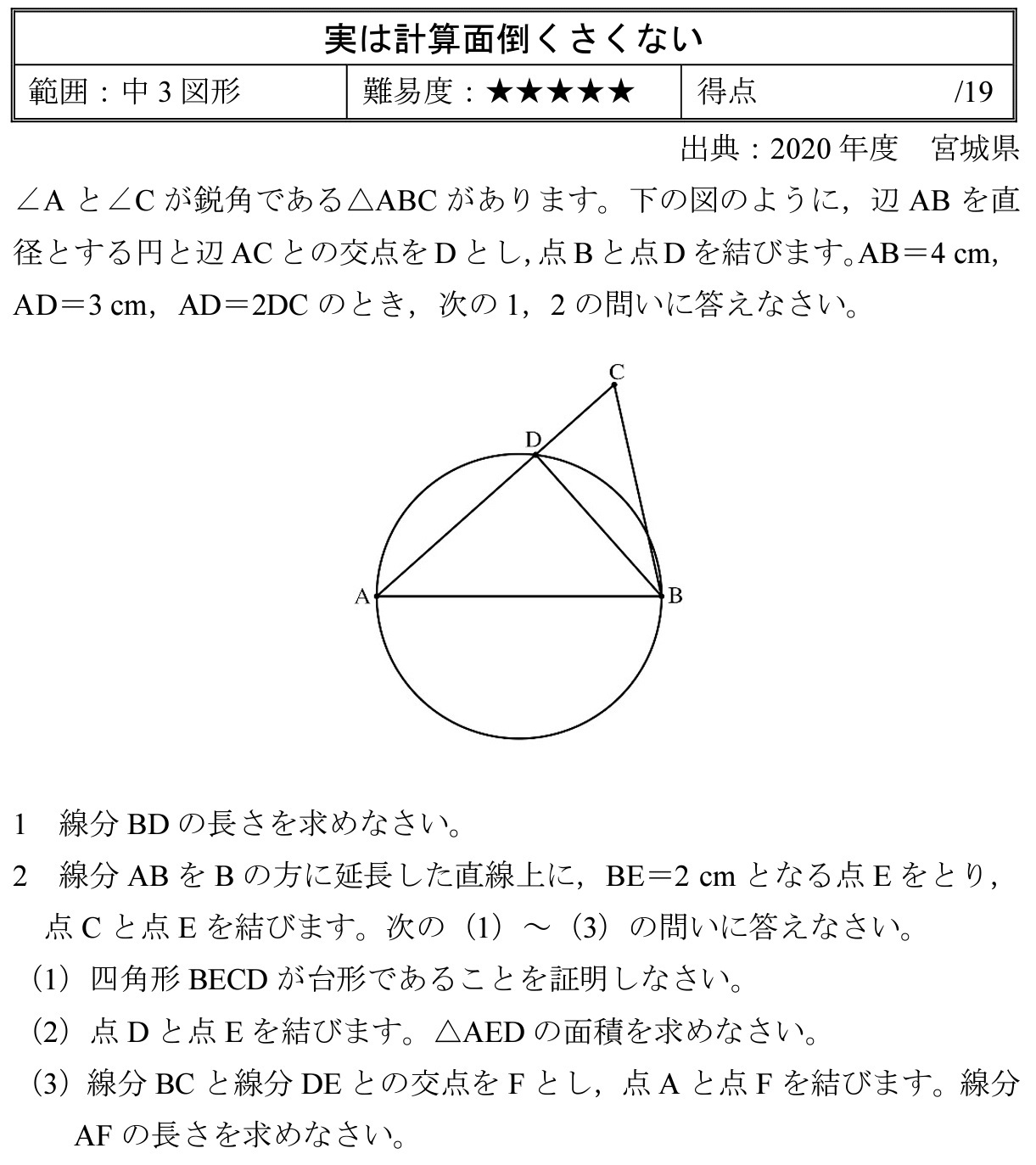



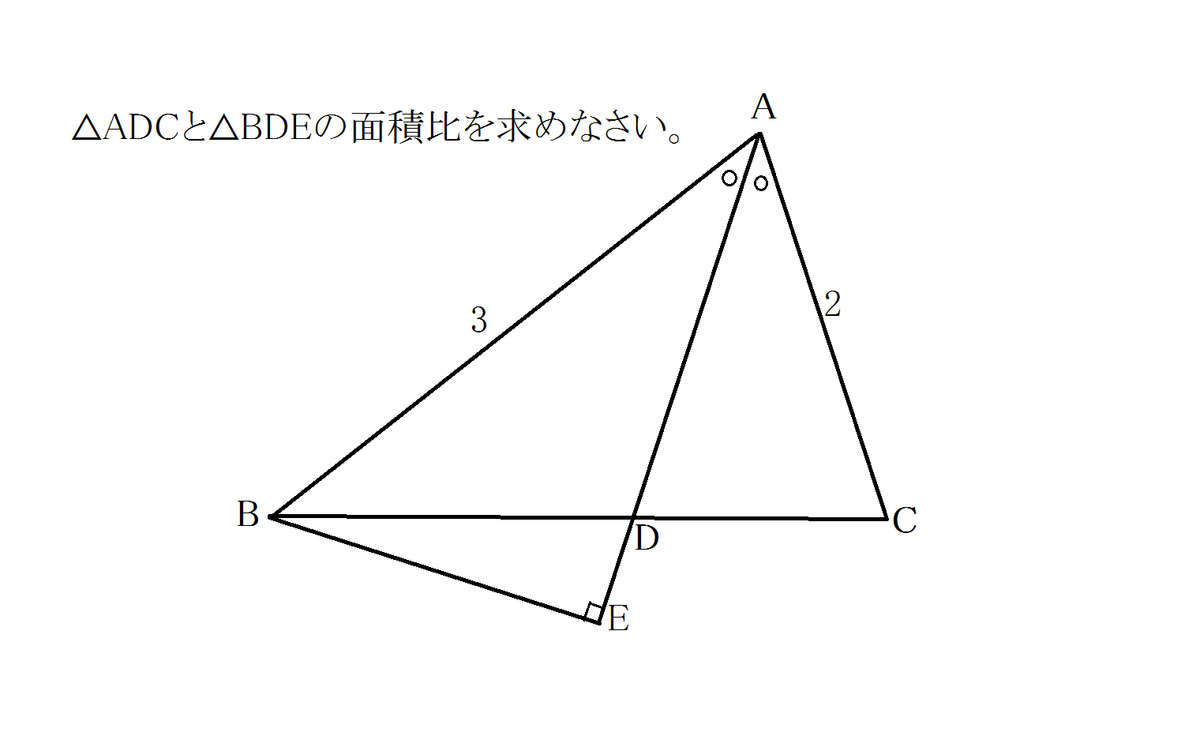
面積比難問 チェバの定理は禁止 年度宮城県 高校入試 数学 良問 難問
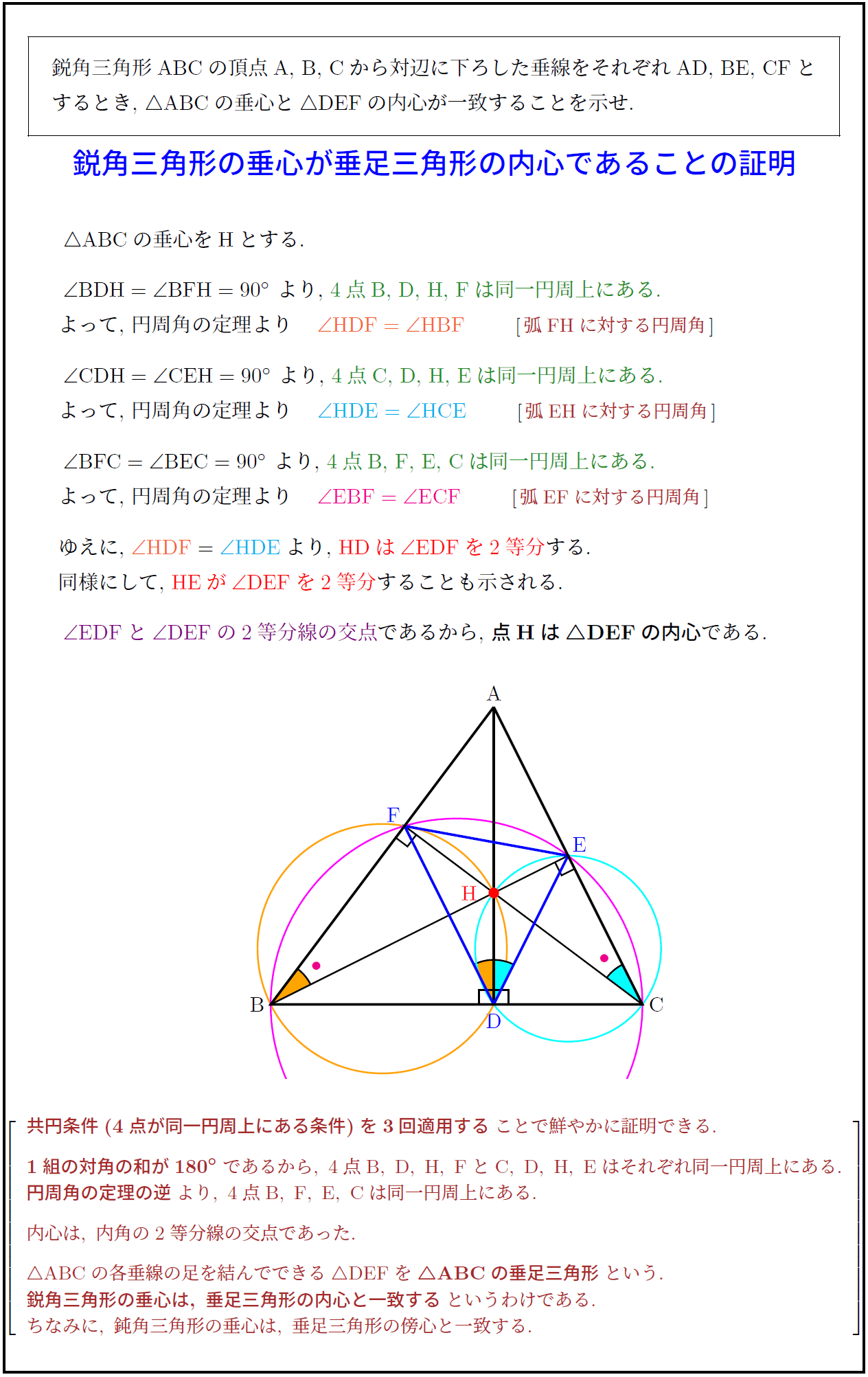



高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




超難問 角度問題です エレガントな解法が出来ません 下の図で X 数学 教えて Goo



タレースの定理



0 件のコメント:
コメントを投稿