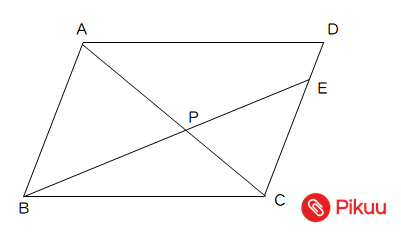
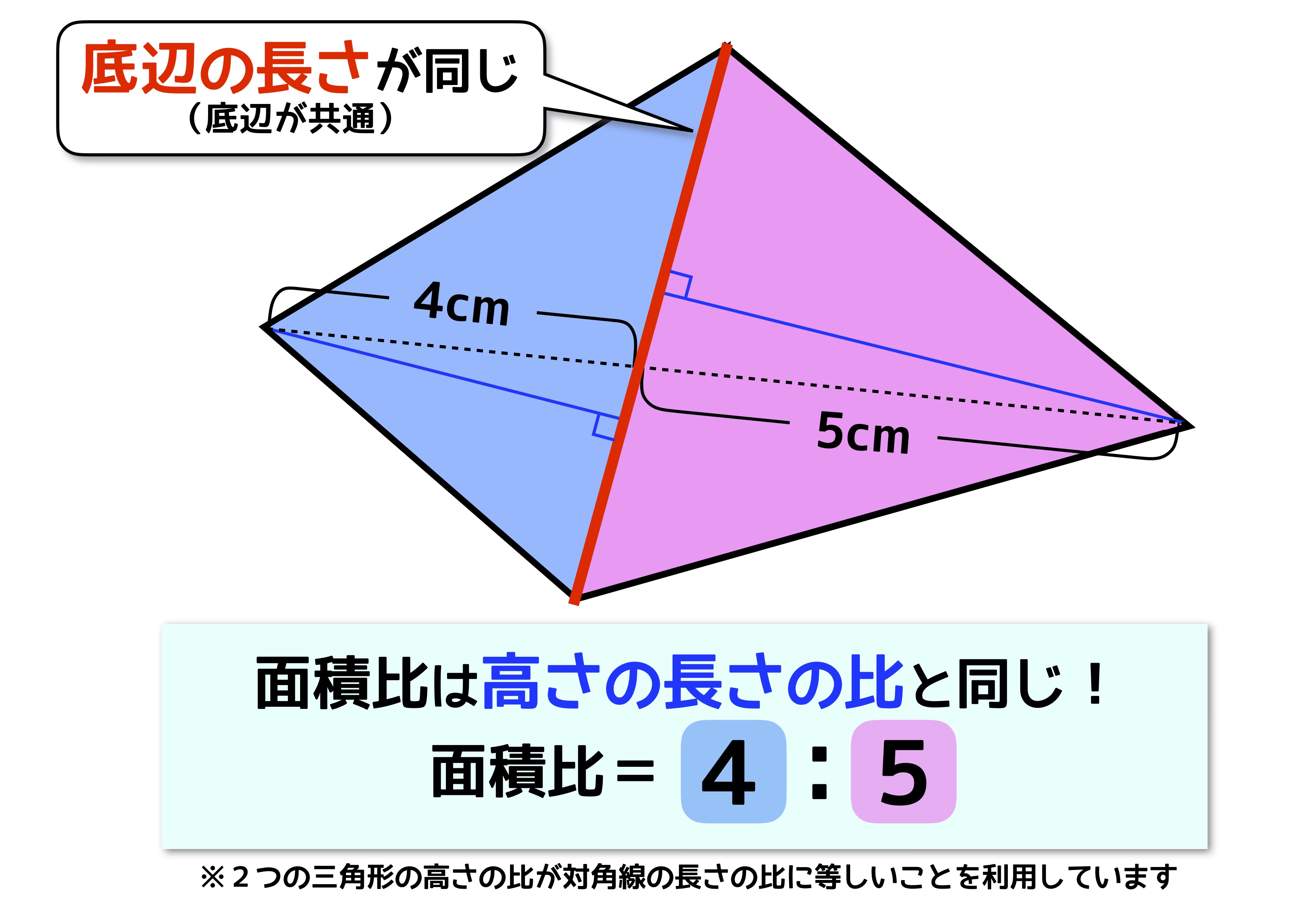
面積比① 右の図の四角形 abcd で,ad°bc,ad:bc=3:5 である。次の 問に答えなさい。 ⑴ ¼aod と ¼cob の相似比を求めなさい。 〔〕 ⑵ ¼aod と ¼cob の面積比を求めなさい。 〔〕 ⑶ ¼boc と ¼doc の面積比を求めなさい。 〔〕反射テスト 面積比 四角形と対角線 01 解答解説 1 下図の四角形の内部に面積比を書き込め(s 級40 秒;「相似ではない」2つの四角形があります。面積比を求めてください。 高さがhで共通しています。よって面積の値は Aの面積 a×h=ah Bの面積 b×h=bh です。面積比=ahbh=abです。つまり高さの等しい四角形の面積比は「底辺の比率」と等しくなります。これは三角形でも同様です。

平面図形の苦手を解消 三角形の面積比 基本編
四角形 対角線 面積比
四角形 対角線 面積比-三角比を用いて、図形の辺の長さや面積を計算する練習をします。 高校数学Iで学習します。 三角比のまとめ的な内容なので、センター試験をはじめとして、どこでもかなり高い確率で出題されます。数Iだけ必要な人にもおすすめです。 経過 date,17,8,9,a 三角形の計量2を追加しました。1辺が 四角形abcdの面積は 8+75=155㎠ よって、 答え 155㎠ 例題6 下の図のような台形abcdがあります。点pは、頂点aより出発して台形abcdの辺上を秒速2cmの速さで、頂点b、頂点c、を通って頂点dまで進みます。11秒後の四角形abcpの面積を求めなさい。 解説



三角形 四角形の面積比 中学から数学だいすき
面積比S1:S2を求める。 ∠AOB=θ ,∠BAP=φ とおくと、 S1=(1/2)absinθ,S2=(1/2)pa+qb-a+bsinφ ここで、cosφ=(pa+qb)・(-a+b)/pa+qb-a+b より、 cosφ=B/A とおくと、 ={pa+qb-a+b}2=pa+qb2-a+b2 =(p2a2+2pqa・b+q2b2)(a2-2a・b+b2) 先ほどの面積公式には h (高さ)が含まれているのですが、三角比を用いることで h を用いずに面積を計算します。 ∠ACB = θ とします。 (図の赤色の角度です。第277問 2つの四角形の面積比 図形ドリル 5年生 6年生 正方形 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。
高さが共通で、底辺affe=56なので面積比は56 ≫ 次に adeと bdeについて ≫ 高さが共通で底辺addb=31 ≫ よって面積比は31, ade=11とすると bde=33 ≫ adf=5,四角形dbef=336=39 よって adfと四角形dbefの面積比は539 5 6 ⑤ ⑥ 1 3 33面積比2 解説 bddc=abなら 面積比 abd adc=ab a b c d bddc=abなら 面積比 abe ace=ab a b c d e 1 図の abcdでeはabの中点、bffc=53である。このとき aegと四角形ebfgの面積比を求めよ。 a b c d e f g 対角線bd,acをひき交点をoとする。またacとedの交点をh, bdとafの交点をiとする。第8問 四角形の対角線 図形ドリル 対角線 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を取り上げています。
「高さの等しい三角形や四角形の面積比=底辺の長さや(上底+下底)の長さの比」 となることを利用して解く問題です。 三角形abeの面積:台形aecdの面積 =底辺be×高さab÷2:(上底ad下底ec)×高さab÷2 =底辺be:(上底ad下底ec)1図形の基本単位は三角形 2四角形は三角形に分割する 3補助線は1本引いただけで考えてみる 4候補の数だけ図を書いてみる 5高さの等しい三角形の面積比=底辺の比 という、5つの大切なポイントが復習できます。 「平面図形と比」の問題が苦手という場合、 テトラード(正四角形)から先は初期設定では用意されていません。 まず最初に「類似色」の状態にします。一番外側のサブカラーを広げます。 そのまま反対側の位置で2色が重なるまで持っていきます。補色の位置になります。 これでテトラードの正四角




中3 数学 6 7 相似比と面積比 平行四辺形 Youtube



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
面積比 = 1 2 :3 2 = 1:9 1:9 = 5: x x = 45 四角形Bの面積は、45cm 2ホーム 図形と計量 対角線と 四角形の面積 数学Ⅰ : 図形と計量 対角線と四角形の面積 数式の表示がおかしいときは こちらをご覧ください。 例題 (1) 図のような四角形 1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ これは全体(abc)-pqrtの周りの三角形でできそうですね。 ・三角形bca:三角形brq=(3×3):(1×1)=9:1 三角形abcの比率はすべて9で揃っているのでそのままいけます。 四角形pqrtの面積比=三角形abc-aptーbrqーcrt
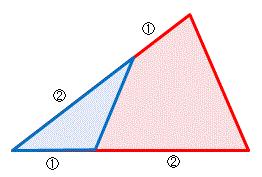



正方形の中の正方形 各辺を一定の比率で分けます



面積比 長さ比 これが中学入試に出た図形問題
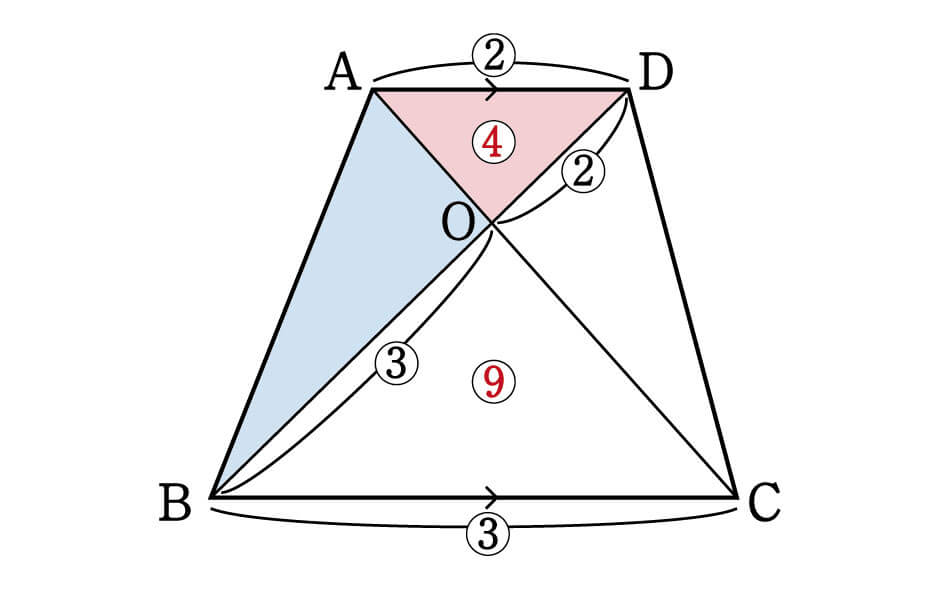
相似な三角形から面積比を考える まずは基準となっている oadの面積をsとして考えていきます。 この台形の中から相似な三角形を探していくと 対頂角や錯角が等しくなることから oadと ocbが相似になることがわかります。 そして、相似比から面積比を考えていくと 2つの三角形の面積比は1 算数 三角形と四角形の面積比 1 38 0 四角形や五角形、六角形も、細かくすると、三角形になるから、 結局、三角形の性質を使って解く問題がほとんどなんじゃ 中学校で習う、三角形の面積と線分の比の関係を導けたわけじゃな では、次は、線分比と面積比の2つ目を考えてみるかのぉ 以下のような場合じゃな 数学おじさ



1




数学 中3 53 相似と面積 応用編 Youtube
面積の比は11×11:8×8=121:64なので、三角形ADEの 面積は64cm 2 。 四角形DBCEの面積は=57cm 2 。凹四角形の角度の関係 a x = 4 角の二等分線に関係する辺の比や長さ b ab ac = be ec = bf cf ae=√ab×ac−be×ec 5 正三角形の辺と高さの比、面積 a h= √3 2 a (面積)= 2 √3 4 a 6 方べきの定理(全3 パターン)c pa×pd=pb×pc pa×pd= pb2 pa×pc=pb×pd 7 頂角が等しい二つの三角形の面積比 b apq abc = ap×aq 四角形の面積の求め方まとめ。タイプ別でわかる公式一覧 このページでは、平行四辺形でも台形でもひし形でもない「ただの四角形」の面積の求め方をまとめています。 関連記事 数に関する記事 円周の求め方と円の面積について 18年11月19日 Tooda Yuuto




相同周長 圓的面積比正方形大 別給我提公式 那是結果不是原因 每日頭條




Formula42 内接四角形の面積比 難関高校合格のための中学数学公式一覧 10秒で解けますか
C 級2 分) (1) 四角形abcd は長方形 最後の三角形の問題の2つに分ける線が3つでその下の台形と1番上の三角形の面積比を求める場合は、、、? ken より 19年1月8日 1005 am 全体の比の合計から上の三角形の比を引いてやればいいね ふう より 19年3月16日 855 pm ペーター何もの???? ふう より 19年3月16日 857 pm ペーター男(補足) ABE+ BCEが、四角形の面積の半分であることは、 ABE= ADE 、 BCE= DCE から明らかであろう。これは、高さの等しい2つの三角形の面積比は底辺の長さの比



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
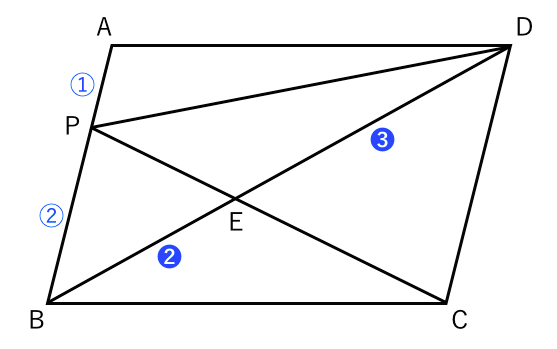



平行からの証明 面積比の問題 苦手な数学を簡単に
四角形の面積(4辺と対角の和から) のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に役に立った 役に立った 少し役に立った 役にまた,円に内接する四角形を2つに割った三角形の面積比について,以下の性質が成立します。 性質3 A D × D C A B × B C = ∣ A D C ∣ ∣ A B C ∣ = D E E B AD\times DC AB\times BC\\=ADCABC\\=DEEB A D × D C A B × BC = ∣ A D C ∣ ∣ A BC ∣ = D E EB平行四辺形の面積は dbcを2倍した値になるので24となります。 以上より rpqの面積を1としたとき、平行四辺形abcdの面積は24となるので 答えは24倍 となります。 ちょっと難しかったけど これも面積比を確実に見ていけば大丈夫な問題ですね! まとめ




六角形面積公式正六邊形 Utvos




平面図形の苦手を解消 三角形の面積比 基本編
つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも 相似な図形ならば、面積比は相似比の \(2\) 乗の比が成り立ちます。 例題1Afdと四角形dbefの面積比を求めよ。 図でapbp=21, bqqc=31, arrc=14である。 a b c p q r abc aprの面積比を求めよ。 abc bpqの面積比を求めよ。 abc pqrの面積比を求めよ。 図の abcdでeはabの中点、bffc=21のとき四角形gebhと abcdの面積比を求めよ。 a b c d e f g h1 2つの三角形の高さが等しいときは,面積の比は底辺の長さの比に等しい. ※ DBE :(四角形) ADEC=8(158)=87 図5 図6 図7 6 相似比が ab となる2つの三角形の面積の比は a 2b 2 になる. 6の証明 5において底辺の比も高さの比も ab になるから, DBE ABC = aa bb = a 2b 2 例4 右図において ADE ABC=49 ADE




成績アップの秘訣 自学学習のススメ 数学の三角形の相似比 ピラミッド型と砂時計型 幼児教育 児童教育



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki
②三角形ABCと四角形PECFの面積の比を最も簡単な整数の比で求めなさい。①apを共通の底辺と考えれば、 高さの比は3:2なので、面積の比もそのまま3:2 ② d:dp=1:2なので、 黄と 緑の面積比も1:2になり、 また四角形dbceの面積比も出せます。⑨ー④=⑤です。 面積比は相似比の2乗 と同じは多角形でも成り立ちます。 台形を三角形に分けた時の面積比のパターン 「長さ」ではなく「相似比」である事に注意してください。 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。




高校数学 円に内接する四角形の対角線の長さと面積 受験の月
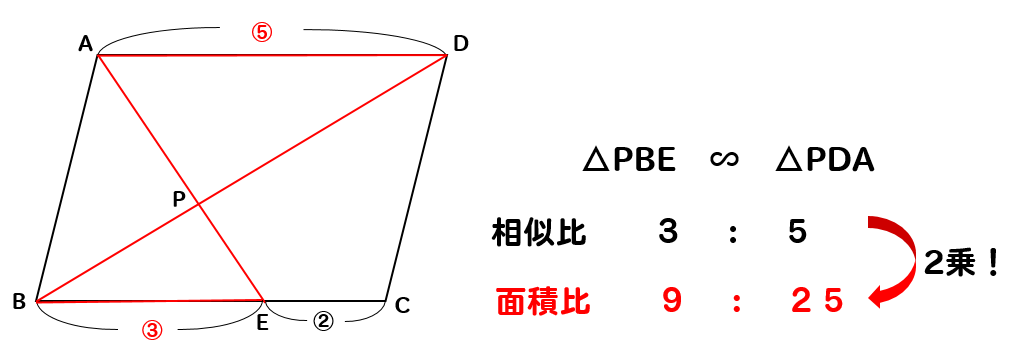



相似 平行四辺形と面積比の問題を徹底解説 数スタ
Bの四角形の幅はna、高さはnhです。 各面積の値は下記です。 相似比が1:nに対して、面積比が1n^2になりました。三角形でも同様です。三角形の面積は底辺×高さ÷2です。 やはり相似比が1:nに対して、面積比が1n^2です。以上より、相似比と面積比の関係は下記となります。平面図形をマスター! 三角形の面積比~応用編その2~ 算数 桂川 紗織 三角形の面積比を解説! 問題演習で平面図形をマスターしよう<応用編その2> 中学受験を目指していく中で、算数で思うように得点できない人の中には「図形問題が特に 三角形の面積比,四面体の体積比にまつわる重要な公式を3つ紹介します。 → 三角形の面積比にまつわる公式たち フランク・モーリーの定理の証明 フランクモーリーの定理: 任意の三角形 a b c abc a bc に対して,3つの角の三等分線どうしが最初にぶつかる点を p, q, r p, q, r p, q, r とおく
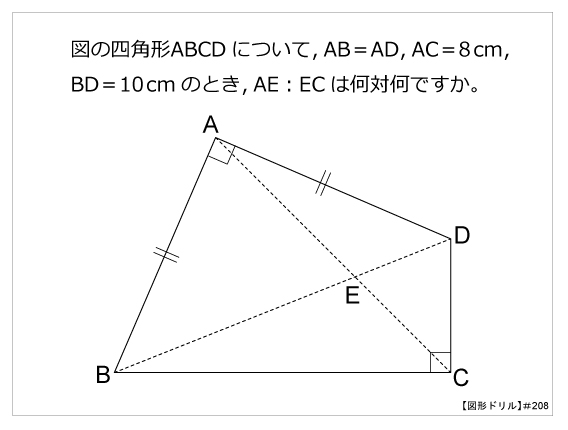



図形ドリル 第8問 四角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
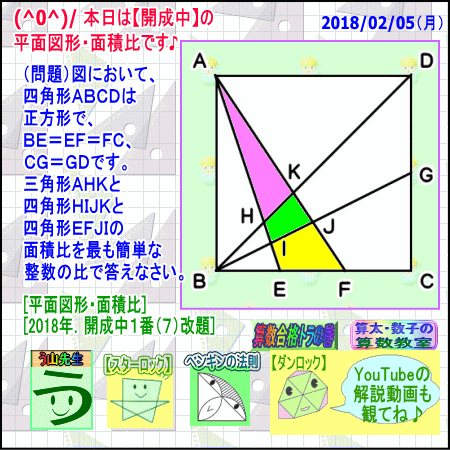
B 級1 分30 秒;(1)三角形AIJと四角形ABCDの面積比を 最も簡単な整数の比で答えなさい。 (2)四角形HIJKと四角形ABCDの面積比を 最も簡単な整数の比で答えなさい。 つぎに四角形fdceと三角形adcの面積の比見てみましょう。 四角形の面積を調べるのは難しいので、違う形に着目します。 fcに補助線を書いて、四角形fdce=三角形fcd+三角形cefとなります。 まず、三角形adcの底辺を辺acとみると、三角形cefと三角形adcの高さは等しく、底辺の比が面積の比になる



1



高校入試対策数学 面積比に関する対策問題 Pikuu
左図の三角形で、bd=6cm,dc=2cmのとき、 abdの面積は abcの面積の何倍か。 (点) 左図で、ad=3cm,db=6cmのとき adeと四角形dbceの面積比を求めよ。 (点) 左図の正方形abcdで、e,fがそれぞれ辺bc,cdの中点のとき、bg:gh:hdを求めよ。また、四角形bcfhの面積は正方形90n°±θの三角比の値 (1) 三角形の 面積から逆算;



平面図形 面積比 開成中2018年 算数 数学 受験 算太数子 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




ベクトル方程式による面積比の問題と解き方
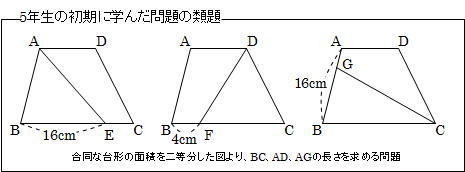



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾
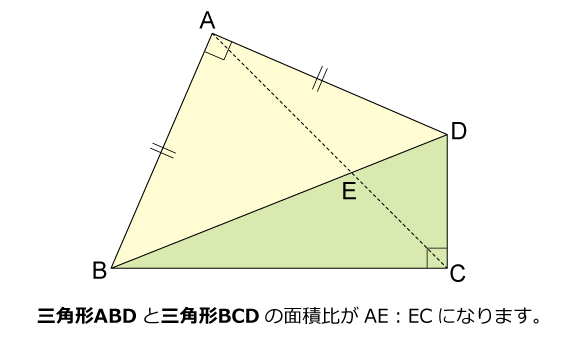



図形ドリル 第8問 四角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦



台形と面積比つづき 四谷大塚 合不合判定予備テストより どう解く 中学受験算数
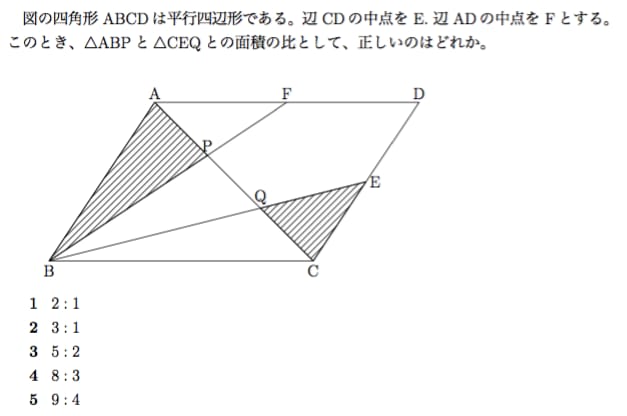



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



三角形と四角形の面積比がわかりません 問題は Ab 9cm 1 Yahoo 知恵袋
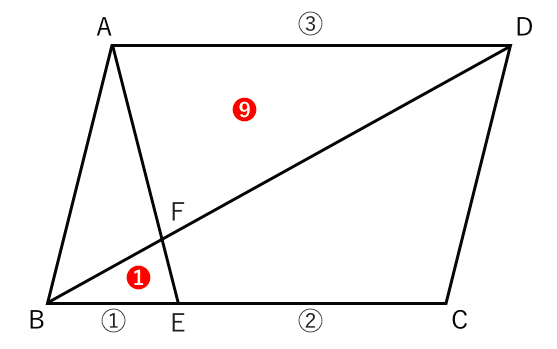



相似な図形 面積比の問題 苦手な数学を簡単に
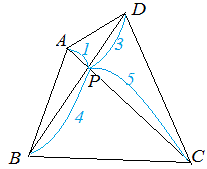



面積比



平面図形と比 平行四辺形の面積比 Next Stageのブログ




高校入試対策数学 面積比に関する対策問題 Pikuu
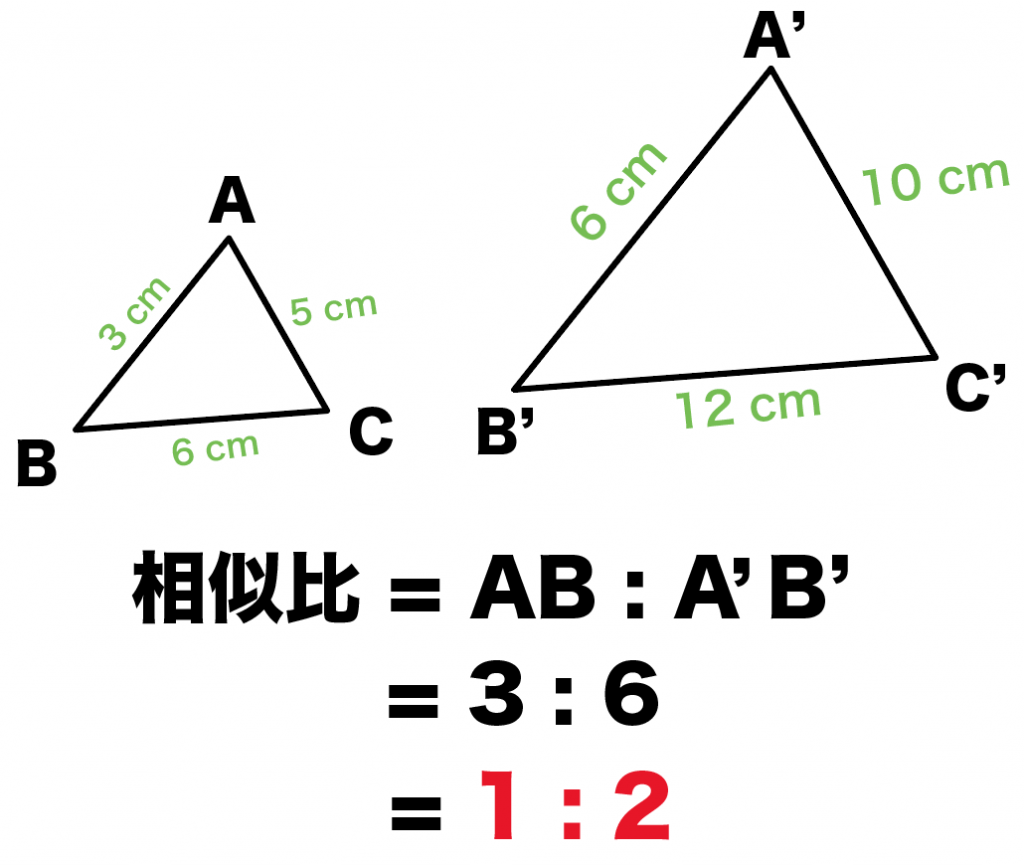



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



中3面積比問 四角形abcdの面積を求めよ Aedの面積比は4 Cebの面 Yahoo 知恵袋



四角形と面積比 べっこう色の記録
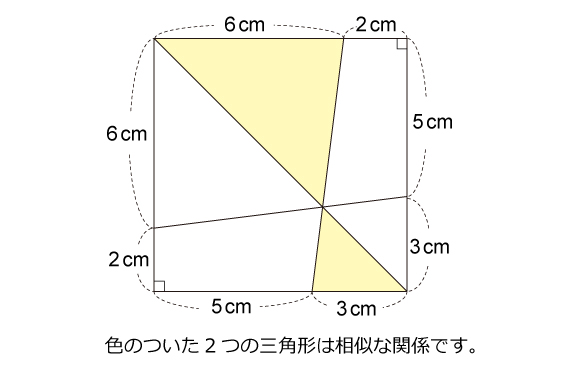



図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
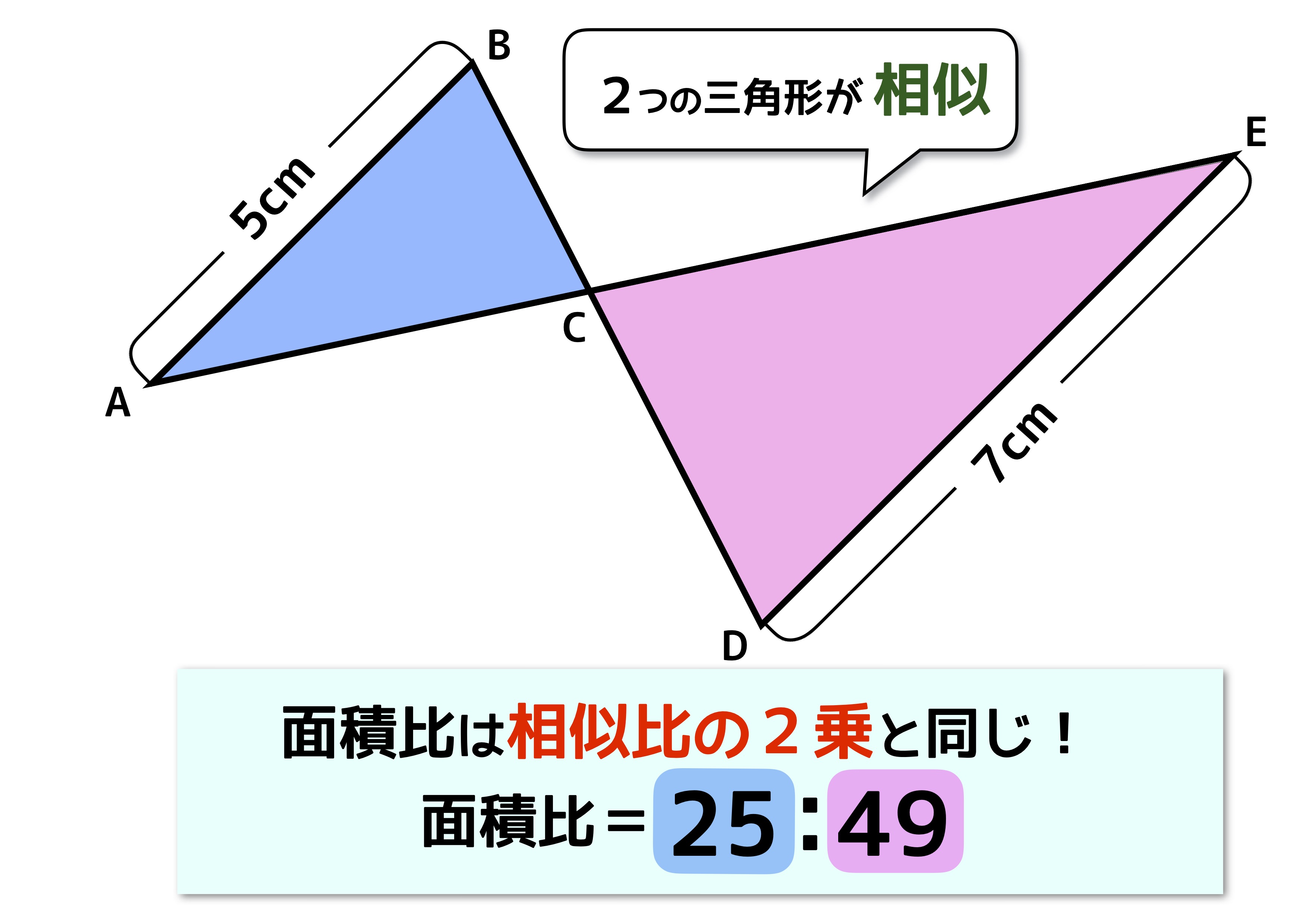



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
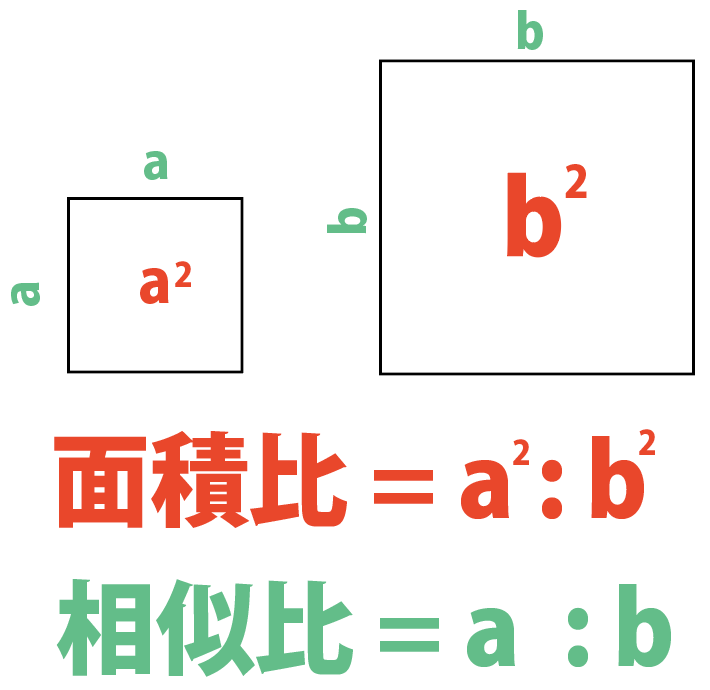



なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



7 4 平行四邊形的面積公式 高市資教中心教材網




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



面積比の計算




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 暇つぶしに動画で脳トレ




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問




3 Abc Debc A Descubre Como Resolverlo En Qanda
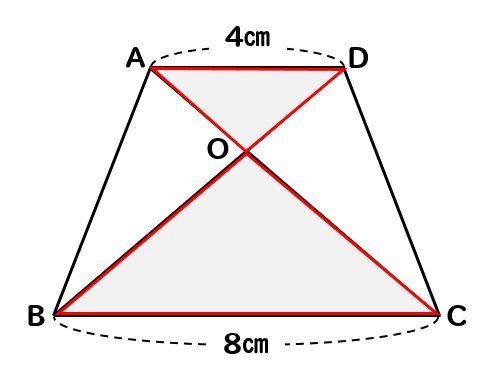



相似 台形と面積比の問題を徹底解説 数スタ




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月



1




L5ahhd13 Beeggcd231cffd3 Descubre Como Resolverlo En Qanda




プロ家庭教師の知力会 照片 Facebook
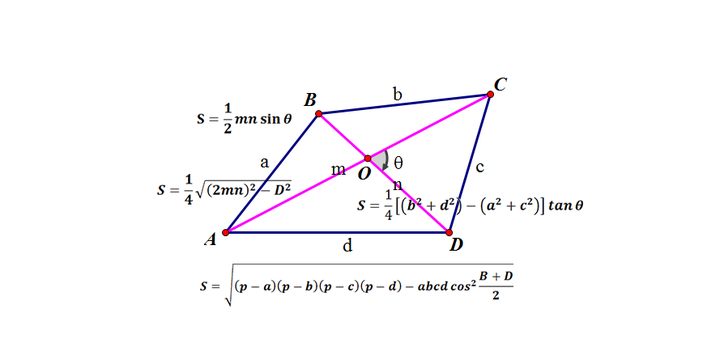



四边形的面积公式 知乎




平面図形をマスター 三角形の面積比 応用編その2
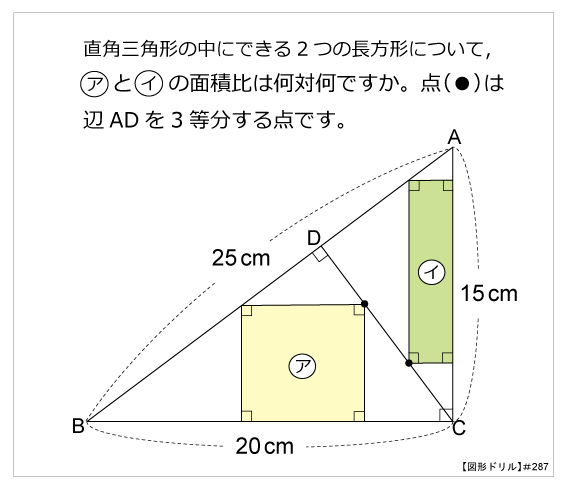



図形ドリル 第287問 長方形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



公立高校入試2019 図形 中学から数学だいすき




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係




解き方教えてください 相似比と面積比 です Clear




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ




Amparo Mate Amparoxmate Twitter




平面図形をマスター 三角形の面積比 応用編その2



三角形 四角形の面積比 中学から数学だいすき



2



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




中3数学 相似な図形の面積比 練習編 映像授業のtry It トライイット



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
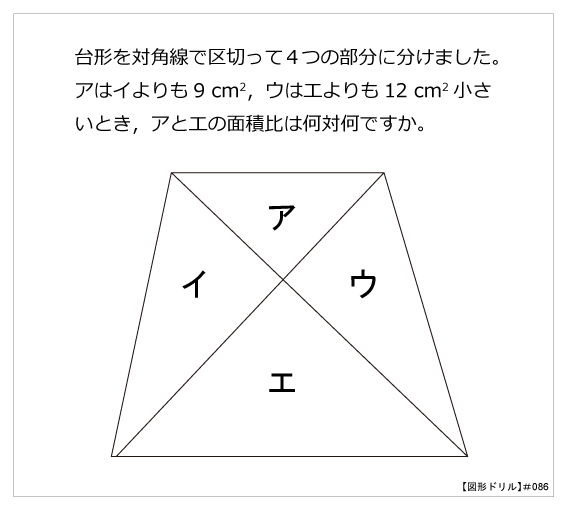



図形ドリル 第86問 台形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
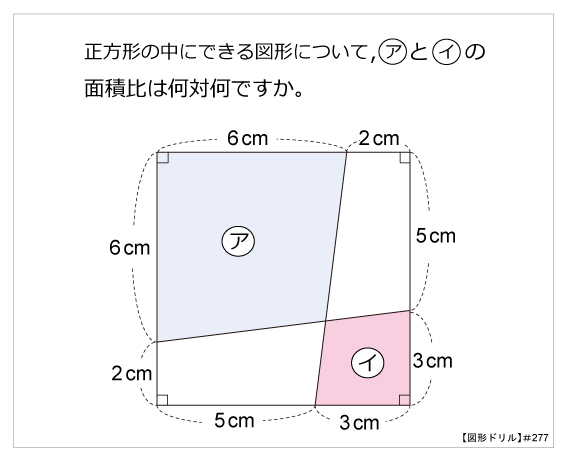



図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



四角形adfeと Abcの面積比を求める問題なのですが Yahoo 知恵袋
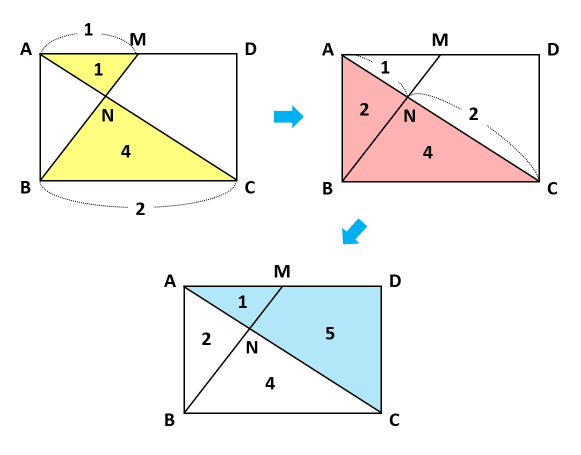



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube



解き方がわからないです ご協力お願い致します 四角形abcdは面 Yahoo 知恵袋




三角形の相似から四角形の面積比へ 開成中学2018入試 算数 問題1 7 テンメイのrun bike



面積比を求める基本 慶應義塾中等部 2012年 算数解法の極意




ポテト一郎 Sur Twitter 円に外接する四角形の面積比




相同周長 圓的面積比正方形大 別給我提公式 那是結果不是原因 每日頭條
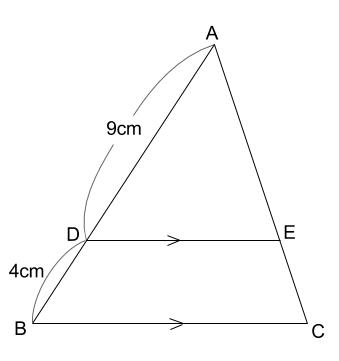



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
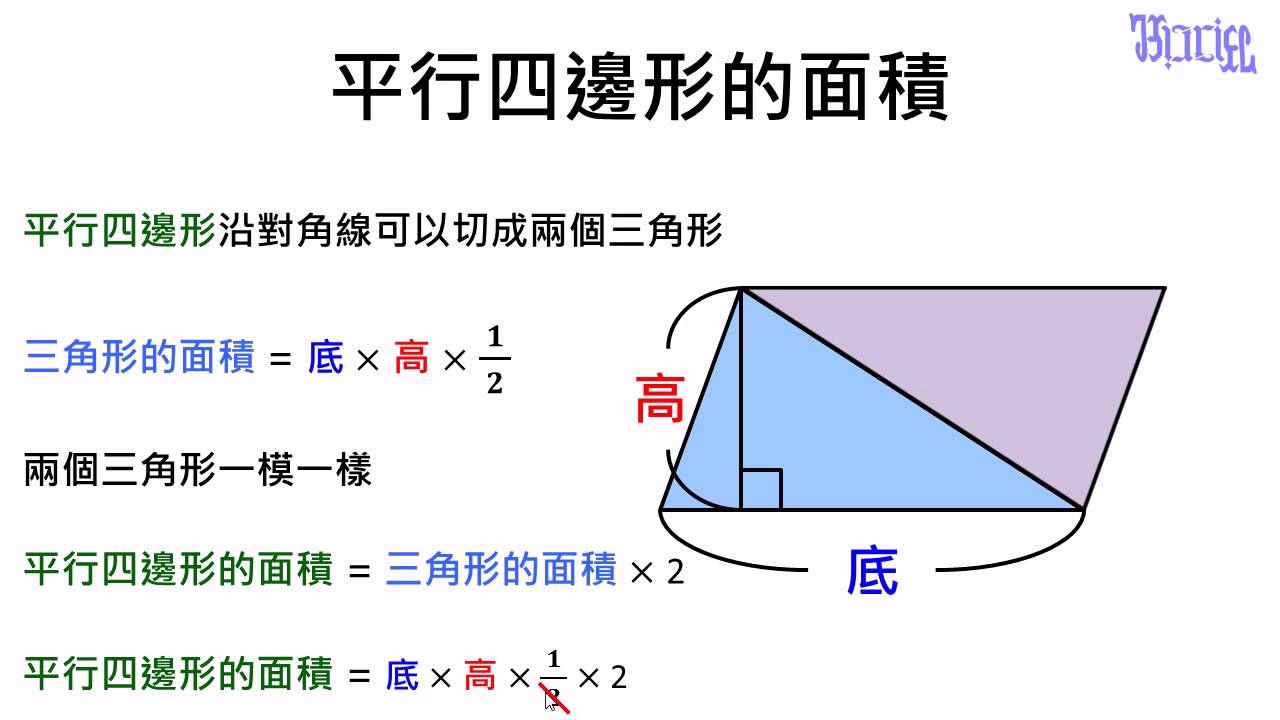



觀念 平行四邊形的面積計算方式證明1 數學 均一教育平台




この面積比を最も簡単な整数比で表してください という問題でした わからないので教え Clear




平面図形の苦手を解消 三角形の面積比 基本編



四角形の重心と面積比




この時の 四角形abpc Pbcの面積比の出し方を教えてください Clear




5 Abcd 2 Adbc 3 D 1 Descubre Como Resolverlo En Qanda



不规则四方形面积 信息评鉴中心 酷米资讯 Kumizx Com




三角比




プロ家庭教師の知力会 照片 Facebook
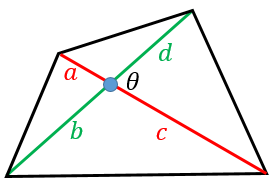



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




平面図形をマスター 三角形の面積比 応用編その2




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
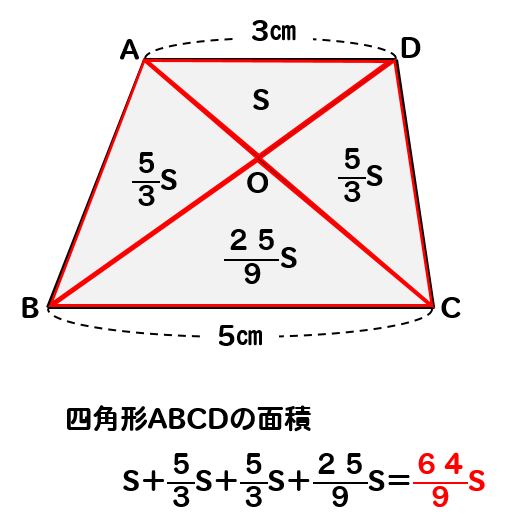



相似 台形と面積比の問題を徹底解説 数スタ



熊先生の学習法



1



みんなの算数オンライン 中学受験 5年 相似比と面積比3 相似の利用3 トレーニング




平面図形の苦手を解消 三角形の面積比 基本編




相似 平行四辺形と面積比の問題を徹底解説 数スタ




中3数学正四角錐の母線長頂点を共有する三角形の面積比 三角錐の体積比 05 03 Youtube



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



面積比 長さ比 中学受験ー算数解き方ポータル




なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく




平面図形の苦手を解消 三角形の面積比 基本編



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
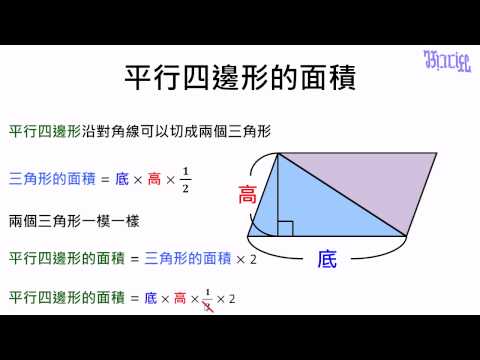



觀念 平行四邊形的面積計算方式證明1 數學 均一教育平台
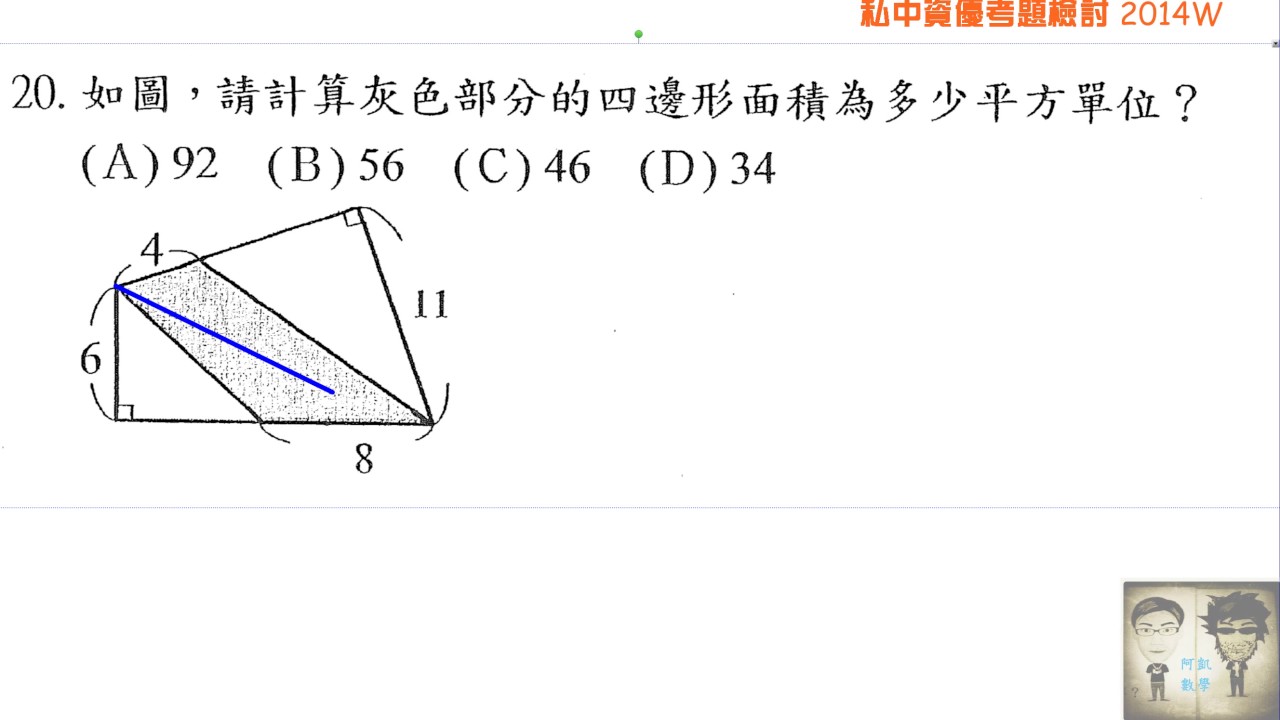



W校資優入學考題 不規則四邊形求面積問題 Youtube



0 件のコメント:
コメントを投稿