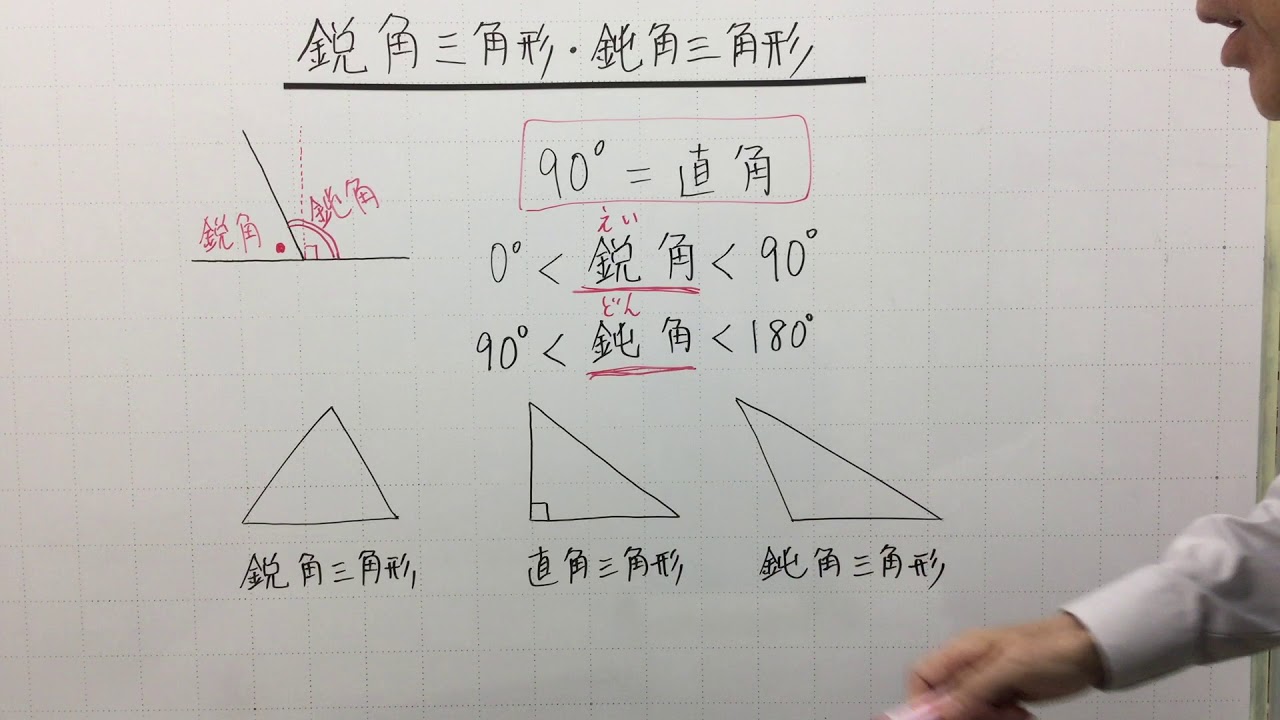
鋭角三角形、鈍角三角形とは 鋭角(えいかく)の「鋭」は「するどい」とも読みます。 鋭角三角形 とは、1番大きい角度が「するどい」($90^{\circ}$ より小さい)三角形のことです。 鈍角(どんかく)の「鈍」は「にぶい」とも読みます。二 等辺 三角形 ☏ 二等辺三角形の面積をどうやって求めるの? 考え方のコツは三角定規に着目すること 二 等辺 三角形。 中2数学図形の中でも重要なものの1つ、二等辺三角形について徹底解説! 次の問題です。 今まで「斜辺」で見ていた長さを鈍角三角形 鈍角三角形 (どんかくさんかっけい、 英 obtuse triangle )は、 三角形 の一種で、3つの角のうち、最大角または長辺に対する角が 直角 (90 ° = π /2 rad) よりも大きい 図形 である。 ^ " 鈍角三角形の合同条件 " 東大・京大・一直線 19年11月3日
中2数学 鋭角三角形 鈍角三角形 0991 Youtube
鋭角三角形
鋭角三角形-鋭角三角形(えいかくさんかっけい、英 acute‐angled triangle )は、三角形の一種で、すべての角が直角 (90°=π/2 rad) よりも小さい図形である。 なお、鋭角三角形では、長辺をc、短辺をa,bとすれば、各辺は c 2 < a 2 b 2 の関係となり、また外心や垂心が三角形の内部に生ずる。三角形が鋭角三角形になる確率 平成21 年2 月23 日 ランダムな三角形についての考え方を現代確率論の立場から説明するのがこの ノートの目的である。以下の例はいずれもネット上で提案されている。




鋭角三角形 Wikipedia
直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った / 上野竜生です。3辺の長さが与えられたとき三角形が成立するのか,成立するなら直角三角形か鋭角三角形か鈍角三角形かを判定することについて考えましょう。 言葉の意味 鋭角三角形:すべての角が鋭角(90°未満)である三角形 直角 鋭角三角形は、すべての角度が90°未満の三角形として定義されます。言い換えれば、鋭角三角形のすべての角度は鋭角です。 急性三角形の特性 すべての正三角形は鋭い三角形です。正三角形には、同じ長さの3つの辺と、60°の3つの等しい角度があります。
三角形の種類 三角形は内角の大きさによって,$3$ 種類に分けられます. すべての内角が $90°$ 未満のとき,鋭角三角形と言います. 一つの内角がちょうど $90°$ のとき,直角三角形と言います. 一つの内角が $90°$ より大きいとき,鈍角三角形と言います. 今回は中2数学で習う三角形の分類、鋭角三角形・鈍角三角形・直角三角形の違いについて勉強したいと思います。 鋭角とは? 直角とは? 鈍角とは? 三角形の分類 鋭角三角形 直角三角形 鈍角三角形 三角形の分類に関する問題 問題① 問題② まずはじめに鋭角、鈍角、直角という言葉の意味直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますが
三角形の形状判定 (鋭角・直角・鈍角) の対応動作環境 ソフト名: 三角形の形状判定 (鋭角・直角・鈍角) 動作OS: Windows 10/8/7/Vista/XP 機種: IBMPC x64 種類: シェアウェア :100円鋭角三角形(えいかくさんかっけい、英 acute‐angled triangle )は、三角形の一種で、すべての角が直角 (90°=π/2 rad) よりも小さい図形である。 なお、鋭角三角形では、長辺をc、短辺をa,bとすれば、各辺は c 2 < a 2 b 2 の関係となり、また外心や垂心が三角形の内部に生ずる。$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。 これらに
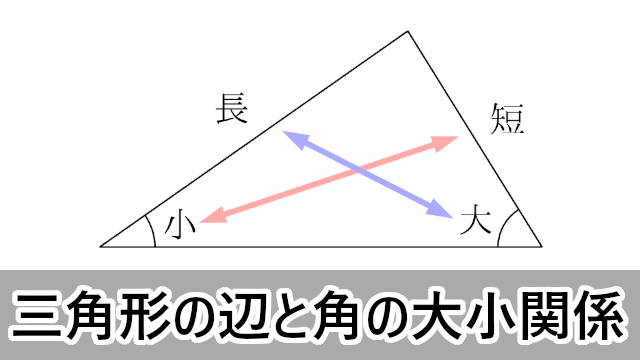



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法
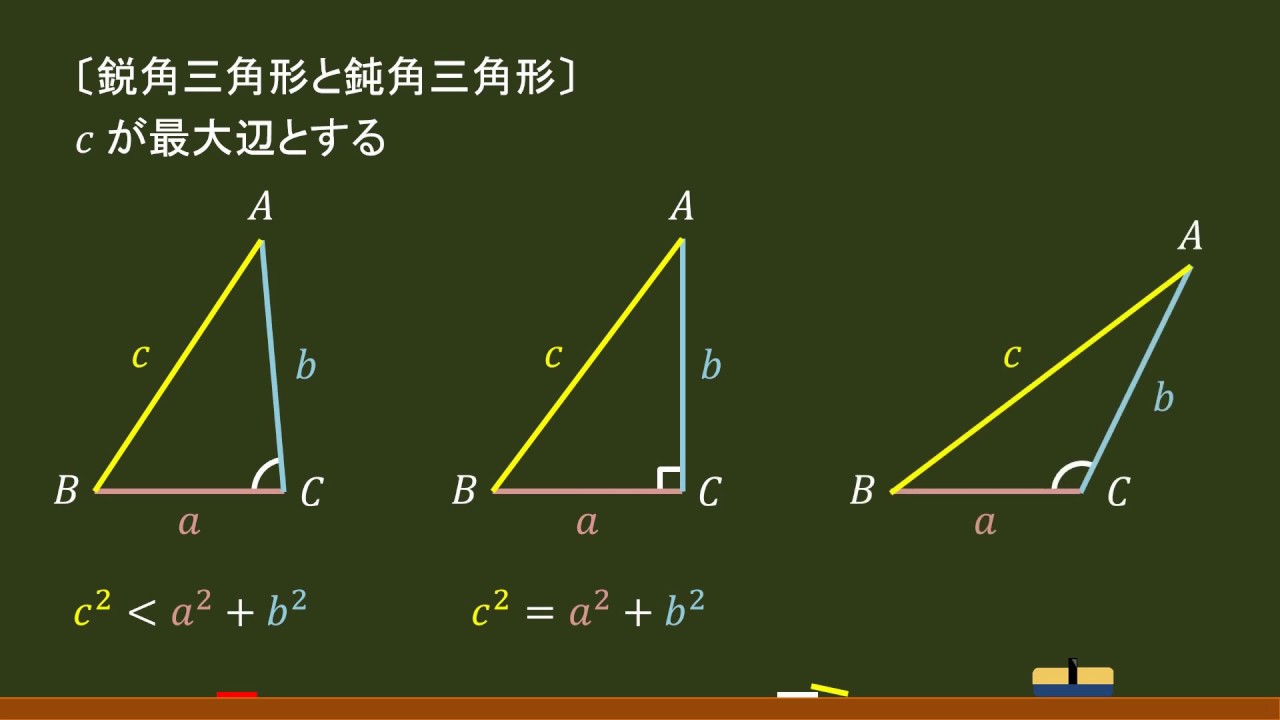



高校数a 図形 鋭角三角形 鈍角三角形の判別方法 オンライン無料塾 ターンナップ Youtube
証明方法は,与えられた三角形が,鋭角三角形,直角三角形,鈍角三角形で少し異なります。 最初に,右の図において,鋭角三角形の証明を行ないましょう。 ① まず,座標平面上の第1象限上にマウスポインタを置き,左クリックしてみて下さい。すると,自動的にその点と原点を結ぶ水色のそれでは,三角形の3 辺の長さから,その三角形を角によって分類してみましょう。 次のような3 辺の長さをもつ三角形は,鋭角三角形,直角三角形,鈍角三角形のどれですか。 5cm,6cm,8cm 6 cm,3cm,14cmゆえに、鋭角三角形と鈍角三角形の出来る確率は等しい。 逆は必ずしも真ならずですが、今度はこれでいいような気がします。 如何なものでしょうか。 ところで、直角三角形は、鋭角三角形と鈍角三角形のどちらに含まれるのでしょうか。




三角比で 鋭角三角形か 直角三角形か 鈍角三角形を見分けるのって 3つの角度をすべて Clear




図形と計量 三角形の面積について 日々是鍛錬 ひびこれたんれん
強磁場中では、離脱可能ダストの半径は磁場入射が壁 に 鋭角 に な るほど大きくなる。 It is clarified that in the case of the strong magnetic field the critical dust radius for the release of the dust increases as magnetic field becomes more acute 必要に応じて環境設定を行ったら 、 三角形直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく



Basicプログラミング
精選版 日本国語大辞典 鈍角三角形の用語解説 〘名〙 内角の一つが鈍角であるような三角形。⇔鋭角三角形。〔数学ニ用ヰル辞ノ英和対訳字書(18)〕となる.直角三角形,鋭角三角形,鈍角三角形のいずれであるかを調べるときに 三角形の成立条件を前提としなければならないのか? 実は,直角三角形,鋭角三角形については,この前提は不要である.a2 ≦ b2 c2 からa < bc を導くことができるからであるお願いします。 鋭角三角形は全ての角が90度より小さい三角形です。 一つでも90度より大きな角があれば鈍角三角形です。 ちなみに、90度ちょうどの角がある三角形を直角三角形といいます



第 6 回大会 08 問題一覧



Renew E School E Tokushima Or Jp Tokushima Jh Joto Wysiwyg File Download 1 243
問題2 鋭角三角形 の内部に点 をとり,線分の長さ和 が最小になるように したい。点 の位置をどこにとればよいか。 ( ヒント 正三角形 , をつくって考える。よって直角三角形の斜辺と 1 つの鋭角がそれぞれ等しいので aop≡ bop 合同な三角形の対応する辺は等しいので ap=bp となる dbc と ecb において bd=ce(仮定) ∠cdb=∠bec=90°(垂線) bc=cb (共通) 合同な三角形の対応する角は等しいので∠dbc=∠ecb 問題 三角形の分類 平面上にどの3点も同一直線上にない 個の点が与えられる. 番目の点 の座標を とする. 個の点の中から異なる3点を選び三角形を作る.その中で鋭角三角形,直角三角形と鈍角三角形の数をそれぞれ求めよ.制約:




鋭角三角形 直角三角形 鈍角三角形かを調べる方法 数学i By ふぇるまー マナペディア
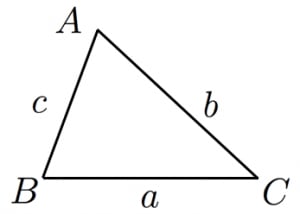



Sinを用いた三角形の面積公式 高校数学の美しい物語
直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。鋭角の三角比 §2 三角比 2.鋭角の三角比 ここでは,前の章で説明した三角比の定義だけでは,まだ理解できないと思いますので,いろいろな三角形を用いて三角比の定義の理解を深めていくことにしましょう。 そこで,もう一度,三角比の定義のお『鋭角三角形をn個の鋭角三角形に分割する。nの最小値を求めよ。』 nの最小値は1です。 この場合であれば鋭角三角形の形に依存せずに分割(しませんが・・・)できます。 ものすごく当たり前です。 重要なのは三角形の形に依存しないと言う事です。



1




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
鋭角三角形ABC の時↓図、 (どの頂点も90°より小) 外心Oは ABCの内部 にある。 直角三角形ABCの時↓図 外心Oは斜辺の中点 にある。 鈍角三角形ABCの時↓図 (90°より大の角を持つ) 外心Oは鈍角の対応する 辺(下図では辺BC)の鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。 表 話 編 歴 多角形 辺の数 1–10 一角形 二角精選版 日本国語大辞典 鋭角三角形の用語解説 〘名〙 三つの内角が、いずれも鋭角である三角形。⇔鈍角三角形。〔数学ニ用ヰル辞ノ英和対訳字書(18)〕




鋭角三角形の鈍角 フォトプリント Zazzle Co Jp



中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット




鋭角三角形 Wikipedia



3




中学2年の数学 動画 鋭角三角形と鈍角三角形の問題 19ch



Triangles



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau



アクセサリーパーツ 鋭角三角形のフレームパーツ 16 40mm 6個セット メール便対応 1 Acp 1311 01 手芸店 Mercerie De Ambience 通販 Yahoo ショッピング



1




1 の 三角形abcが鋭角三角形になる時のxの範囲はどうやって求めるんですか Clear



中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い




高度 三角形 Ja Wikitechpro Com



2



48s96ub7b0z5f Net Sankakuhi Seiritsujouken Katachi




1 の 三角形abcが鋭角三角形になる時のxの範囲はどうやって求めるんですか Clear



鋭角三角形実際にかわいい三角形 ポスター Zazzle Co Jp



2016年 東大数学 理系第4問 三角形をなす条件 鋭角三角形の条件 複素数平面 オンライン受講 東大に 完全 特化 東大合格 敬天塾



鋭角三角形の確率




鋭角のときの 三角比の公式の証明 数学i By Okボーイ マナペディア
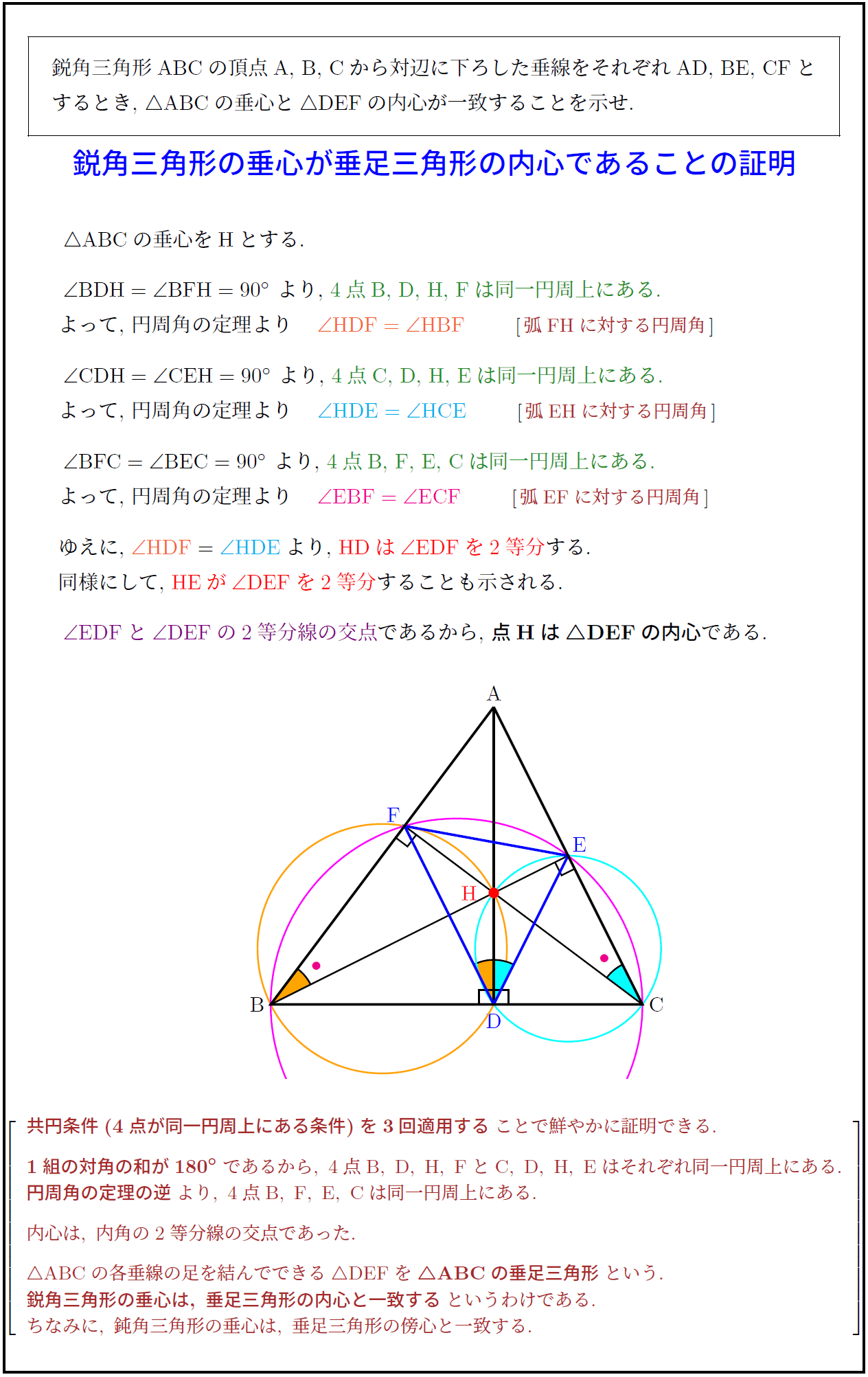



高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い




Ce E D Descubre Como Resolverlo En Qanda




中2 数学 中2 43 鋭角三角形 鈍角三角形 Youtube
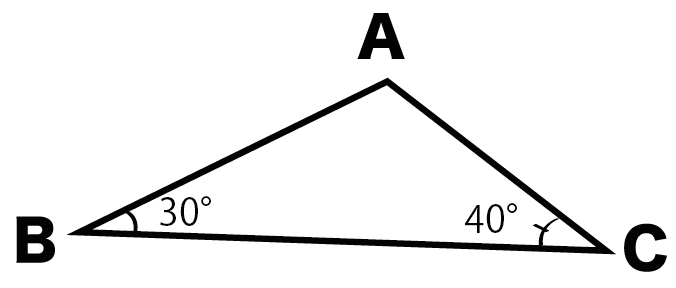



中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく




高校数 三角比 正弦定理 理由 鋭角三角形 オンライン無料塾 ターンナップ Youtube




Kistenkasten723 啓林館の教科書は 小5面積の章は 1 三角形の面積の節 直角三角形 鋭角三角形 2 平行四辺形の面積の節 3 面積の公式を使って 鈍角三角形 などに分かれていています




𝐏𝐮𝐫𝐨 𝐒𝐡𝐨𝐝𝐚𝐢 Abcが鋭角三角形 Ab 2 2 Ac 2 2 Ac 2 Ab 2 Ac 2 Ab 2 2 今回は辺の長さの条件で処理した 別解 Abcが鋭角三角形 Bac P 2 Abc P 2 a P 2 これらを偏角の条件として表す 略 T Co



鋭角三角形abcにおいてa osc Ccosbが成り立つことを証明せよ Yahoo 知恵袋



鋭角とは 1分でわかる意味 定義と求め方 0度 範囲 鈍角との違い
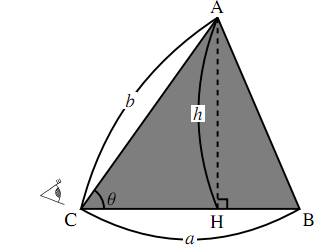



三角形の面積と三角比 数学i フリー教材開発コミュニティ Ftext
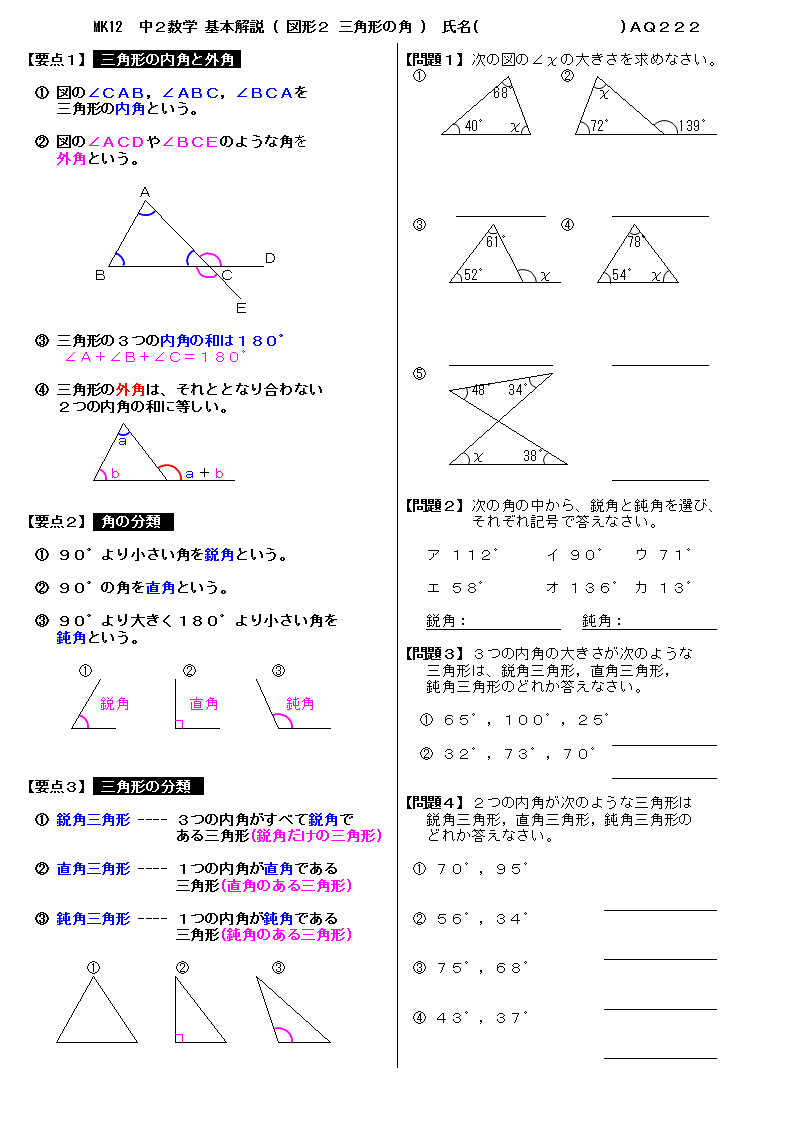



無料 中2数学 基本解説 問題プリント 222 図形2 三角形の角




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月




鋭角三角形 直角三角形 鈍角三角形って何が違うんですか 教えてください Clear



Kadai78




鋭角三角形のイラスト素材




A30 Abc Lihat Cara Penyelesaian Di Qanda




この65番の問題がわかりません Clear




図のように 鋭角三角形abcの内部の点をpとし Acを一辺とする正 人力検索はてな



鋭角三角形 数学入試問題




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




三角形の問題から鋭角について 5 5 7 7 8 8より シータは鋭角と Okwave
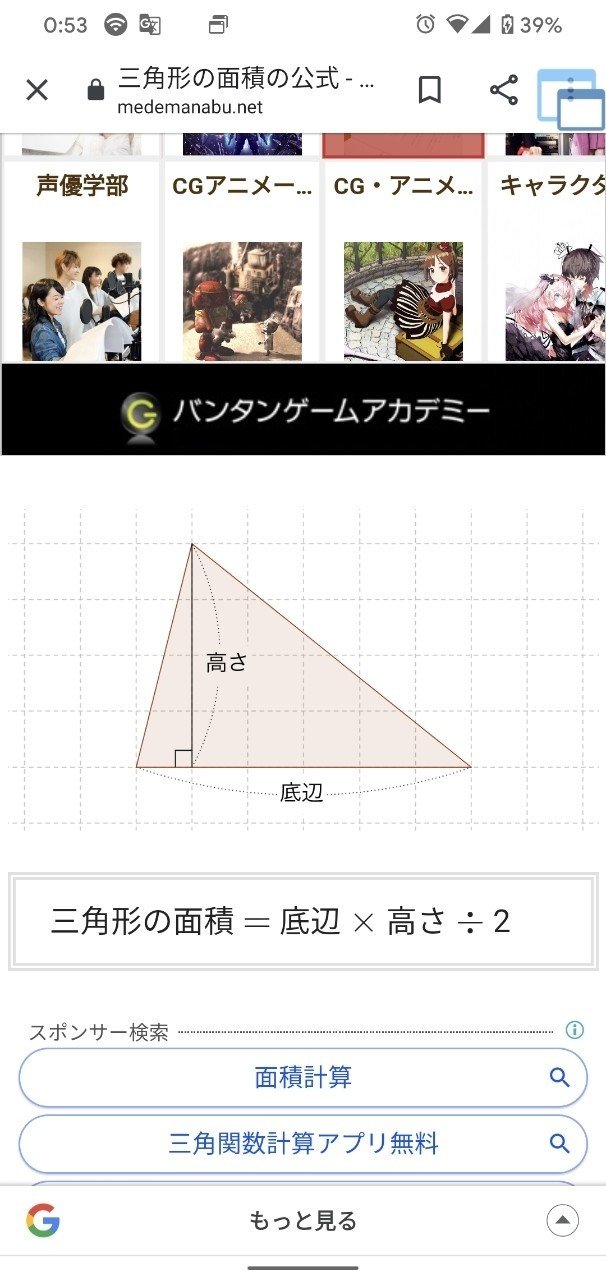



鈍角三角形の面積の求め方がやっと理解できたって話 猿田助 Note
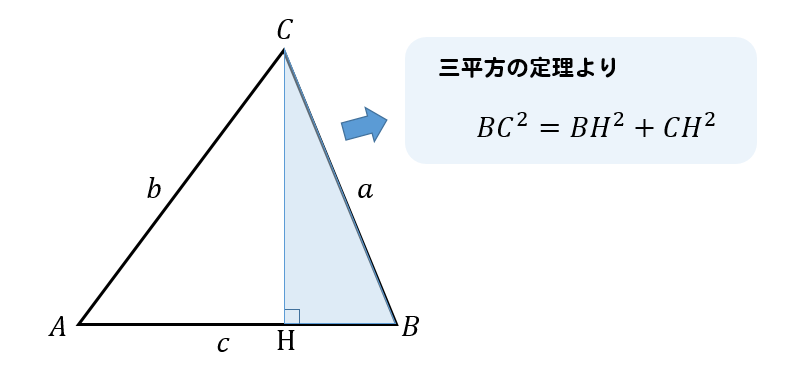



余弦定理の証明 簡単にわかりやすく考えてみよう 数スタ



図形の問題です 図のように 鋭角三角形abcの頂点aか Yahoo 知恵袋



外接円 外心について



Abc 3 Abc Lihat Cara Penyelesaian Di Qanda




鋭角三角形のイラスト素材




A かわいい子供たちカラフルな幾何学的図形アルファベット トレース フラッシュ カード鋭角三角形の英語語彙学習の子供のため のイラスト素材 ベクタ Image




動画 三角形の分類 Youtube




鋭角三角形と鈍三角形正三角形幾何学 三角形 鋭角と鈍角の三角形 角度 角度鈍角 Png Pngwing



鋭角三角形 直角三角形 鈍角三角形はなんですか できれば図で Yahoo 知恵袋
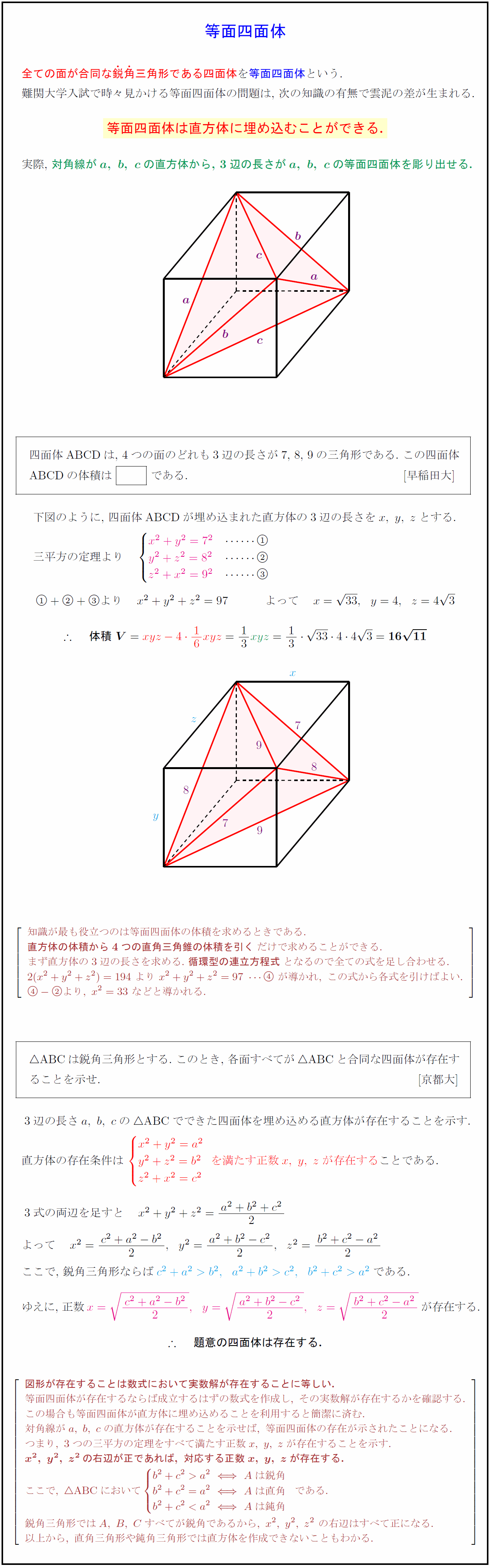



高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月




鋭角三角形




2016年 東大文系数学 第1問 三角形の成立条件 鋭角三角形の条件 領域図示 オンライン受講 東大に 完全 特化 東大合格 敬天塾




中2数学 鋭角三角形 鈍角三角形 0991 Youtube



直角 鋭角 鈍角三角形の判定法 思考力を鍛える数学




なぜこれで三角形が鋭角三角形であることを示せるんですか Clear



中学3年数学平面図形鋭角三角形abcの頂点b Cから辺ac Yahoo 知恵袋




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




鋭角三角形と鈍角三角形の意味と見分け方 具体例で学ぶ数学
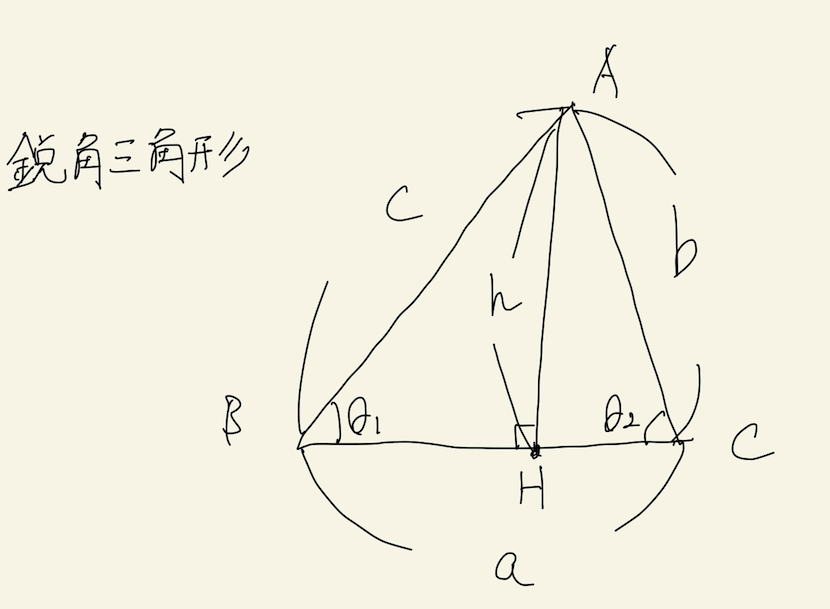



任意の三角形の垂線とその足による内分点の性質 物理u数学の友 質問 悩みに回答します




鋭角三角形abpの辺ab Bp Paの中点をそれぞれmqrとおき 線分mq Qr R Clear
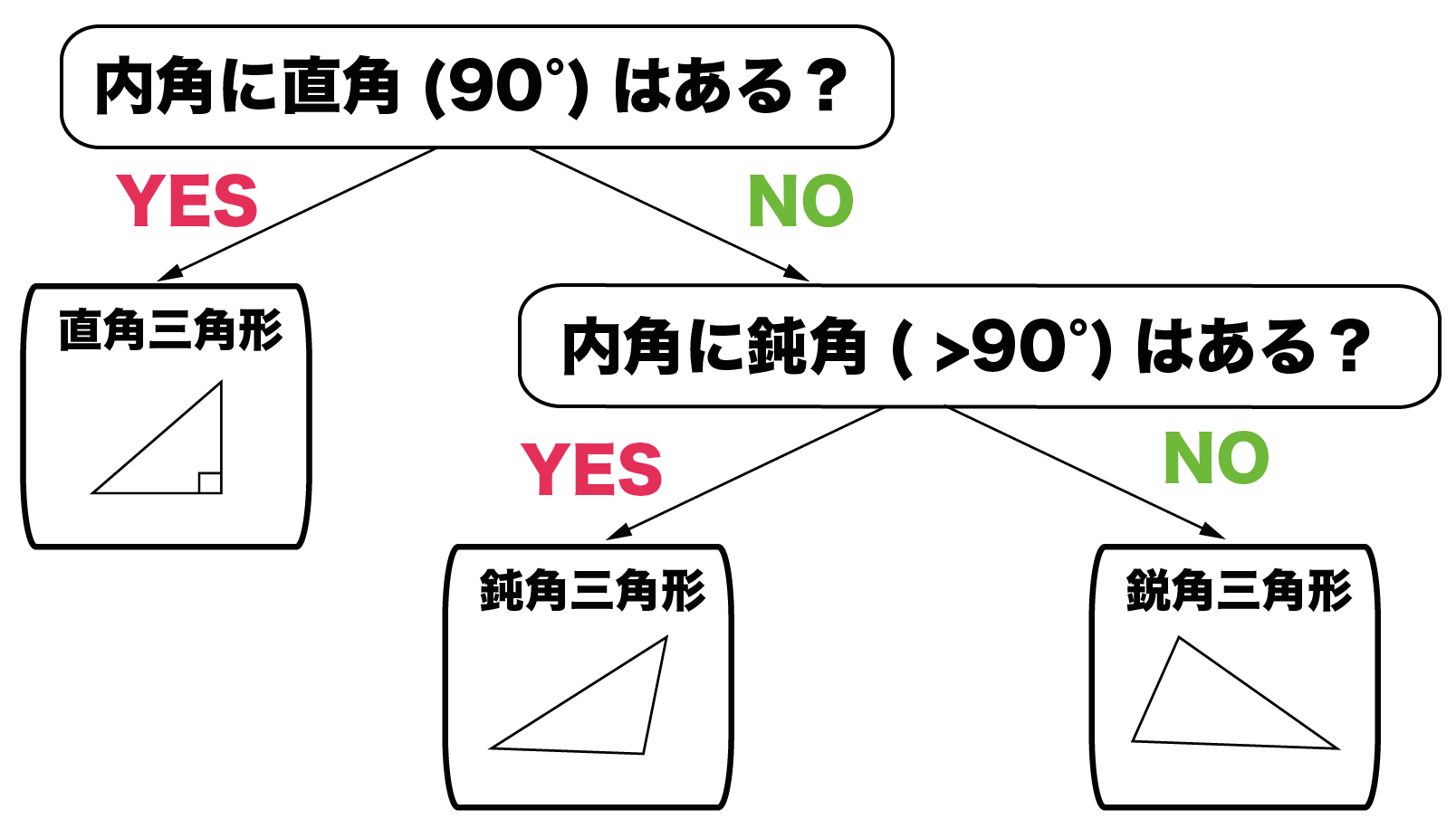



鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
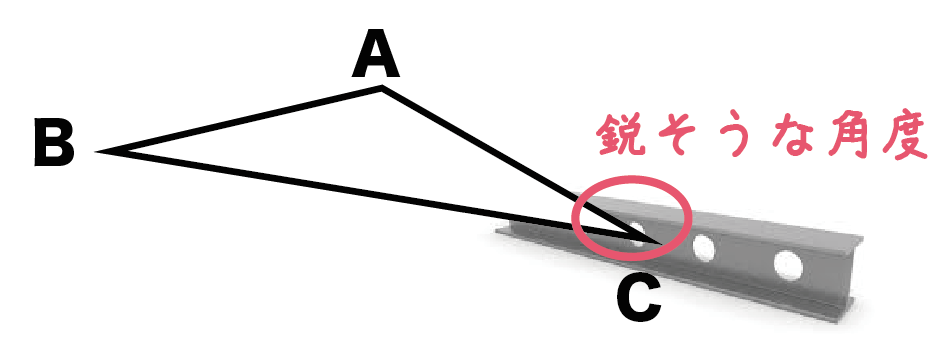



中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく



Studydoctor鈍角三角形 鋭角三角形の見分け方 高校数学 Studydoctor




鈍角三角形 鋭角三角形 直角三角形の違いを詳しく教えてください お願いします Clear
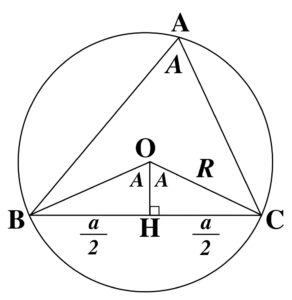



正弦定理とその証明を勉強しよう スタディクラブ情報局




数学 中2 50 鋭角三角形と鈍角三角形 Youtube




三角形の成立条件と鋭角 直角 鈍角三角形の判定 数学の偏差値を上げて合格を目指す



鋭角三角形の周



Triangles



2




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




鈍角三角形 直角 鋭角 鈍角三角形の判定法 思考力を鍛える數學翻譯此網頁 Patry Kdas




14 号 図形板セット Astamuse




京都大学 理系 19年度 第3問 解説 ページ 2 なかけんの数学ノート
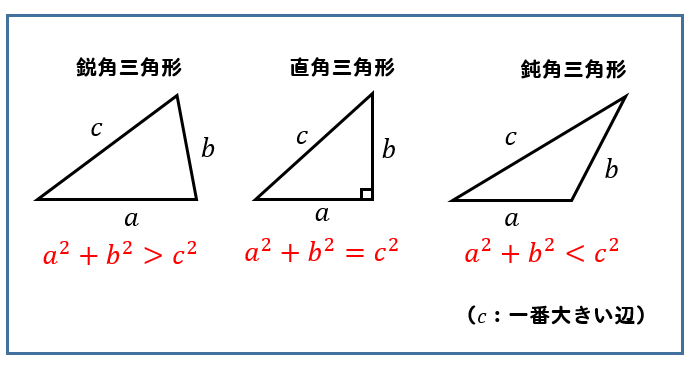



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ
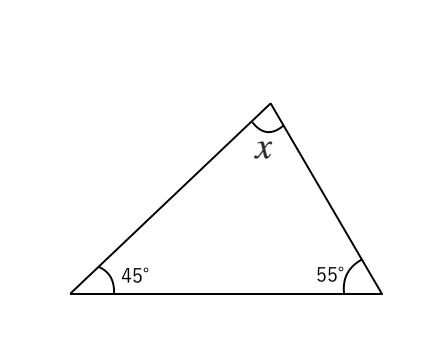



図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく
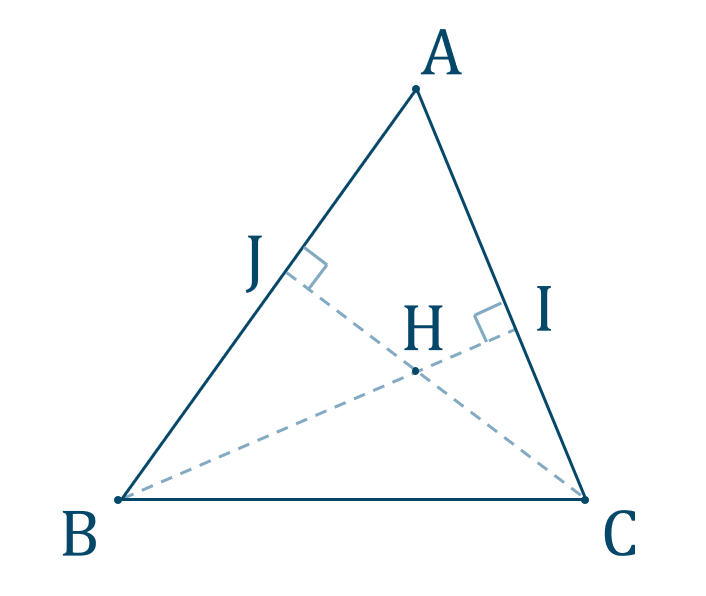



数学a 三角形の垂心の性質の使い方とコツ 教科書より詳しい高校数学




高校数学 三角形の鋭角 直角 鈍角条件 三角形の成立条件3パターン 受験の月



鈍角三角形の分割




第1余弦定理 数式で独楽する



全て の 角 が 90 の 三角形




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強
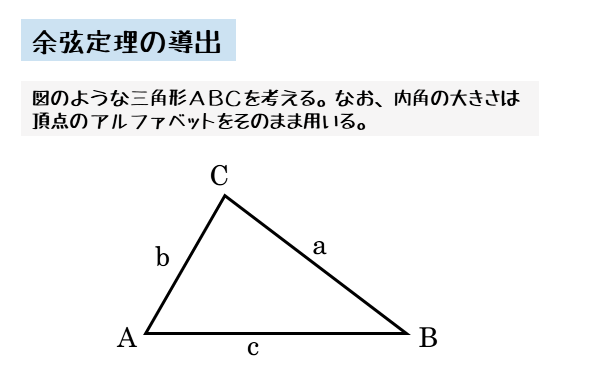



図形と計量 余弦定理について 日々是鍛錬 ひびこれたんれん



鈍角三角形の分割



0 件のコメント:
コメントを投稿